Coupled oscillators
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
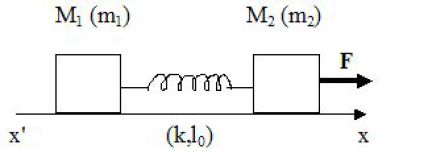
Two masses \(m_1\) and \(m_2\) are attached by a spring of spring constant \(k\) and of relaxed length \(\ell _0\).
They move freely on a horizontal axis (x'x) without friction.
When \(t<0\), the spring is relaxed, the masses \(m_1\) and \(m_2\) are at rest on \(M_{10}\) and \(M_{20}\).
From \(t=0\), a horizontal constant force \(\vec F = F\ \vec u_x\) is exerted on \(M_2\).
Let \(x_1(t)=M_{10}M_1\) and \(x_2(t)=M_{20}M_2\).
Question
Find \(x_1(t)\) and \(x_2(t)\).
Indice
Apply the second law of Newton on the two masses.
Solution
We apply the second law of Newton on each of the two masses, we project it on the axis (Ox) :
\(m_1 \ddot x_1=k(\ell_0 +x_2 -x_1 - \ell_0)=k(x_2 -x_1 )\)
\(m_2 \ddot x_2=-k(x_2 -x_1 )+F\)
We sum the equations :
\(m_1\ddot x_1 + m_2 \ddot x_2 = F\)
We integrate and take the initial values into account :
\(m_1 x_1+m_2 x_2=\frac{1}{2} F t^2\)
We can write the equations as :
\(\ddot x_1=\frac {k}{m_1}k(x_2 -x_1 )\)
And :
\(\ddot x_2=-\frac {k}{m_2}(x_2 -x_1 )+\frac{F}{m_2}\)
By subtracting these equations :
\(\ddot x_2-\ddot x_1=-k(\frac {1}{m_1}+\frac{1}{m_2})(x_2 -x_1 )+\frac{F}{m_2}\)
We note :
\(\Omega ^2= k(\frac {1}{m_1}+\frac{1}{m_2})\)
Then :
\((\ddot x_2-\ddot x_1)+\Omega^2(x_2 -x_1 )=\frac{F}{m_2}\)
The solution is :
\(x_2-x_1=Acos\Omega t + Bsin\Omega t + \frac{F}{m_2 \Omega^2}\)
Using the initial values :
\(x_2-x_1=\frac{F}{m_2 \Omega^2}(1-cos\Omega t)\)
From which we deduce\( x_1(t)\) and \(x_2(t)\), since we know their sum and their difference.