Without source :

Let's consider an homogeneous body (in fact, most of the time a liquid or a solid one) with \(\rho\) its density, \(\lambda\) its thermic conductivity and \(c\) its heat capacity.

Those quantities are supposed to be constants.

In a first time, let's suppose that there is no sources able to provide heat locally in the medium.

Finally, we keep working in a single dimension named \((Ox)\).

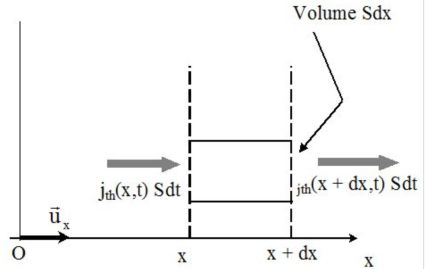
Let's apply the first principle of thermodynamics to a small volume \(dSdx\) :

\(dU = \delta Q\)

Where \(dU\) is the variation of the internal energy of the volume and \(\delta Q\) the conduction thermal flow.

The internal energy of the volume is, at time \(t\) :

\(U(x,t) = \rho dS dx\ c\ T(x,t)\)

So :

\(dU = \rho dSdx\ c\ \frac{{\partial T(x,t)}}{{\partial t}}dt\)

Furthermore, the conduction thermal flow is :

\(\delta Q = {j_{th}}(x,t)dSdt - {j_{th}}(x + dx,t)dSdt\)

Or :

\(\delta Q = - \frac{{\partial {j_{th}}(x,t)}}{{\partial x}}dSdtdx\)

The first principle of thermodynamics finally results in :

\(\rho dSdx\ c\ \frac{{\partial T(x,t)}}{{\partial t}}dt = - \frac{{\partial {j_{th}}(x,t)}}{{\partial x}}dSdtdx\)

Finally : (equation of conservation of energy without source)

\(\rho \ c\ \frac{{\partial T(x,t)}}{{\partial t}} = - \frac{{\partial {j_{th}}(x,t)}}{{\partial x}}\)

With heat sources :

Let's suppose now that heat sources are present in the medium.

Let's note \(p_s (x,t)\) the algebric volumetric power of the sources.

Example (Joule heating) :

If an electrical current runs through the material, the small volume \(dSdx\), with \(dR\) its electric resistance, with \(di=jdS\) running through it, receives during \(dt\) the energy :

\(\delta Q = dR\;{(di)^2}dt = \frac{1}{\sigma }\frac{{dx}}{{dS}}{j^2}{(dS)^2}dt = \frac{1}{\sigma }{j^2}dxdSdt\)

Hence the volumetric power due to Joule heating :

\({p_s} = \frac{{{j^2}}}{\sigma }\)

We can also write (see the lesson about electromagnetic energy and Local Ohm's law) :

\(p_s=\vec j . \vec E=\sigma E^2=\frac {j^2}{\sigma}\)

With sources, the energy balance becomes :

\(\rho dSdx\ c\ \frac{{\partial T(x,t)}}{{\partial t}}dt = - \frac{{\partial {j_{th}}(x,t)}}{{\partial x}}dSdtdx + {p_s}(x,t)dSdxdt\)

That is to say :

\(\rho \ c\ \frac{{\partial T(x,t)}}{{\partial t}} = - \frac{{\partial {j_{th}}(x,t)}}{{\partial x}} + {p_s}(x,t)\)