Consider a thermodynamic system \((S)\) at rest in the laboratory reference (R) (gas in a vessel, solid, ...).

The internal energy is a state function of a system : it is defined in the equilibrium state of the thermodynamic system.

\(U = \sum\limits_{Particles} {{e_{{c_i}}}} \;\;\;\;+\;\;\;{E_{p,{\mathop{\rm mut}} \;int}}\)

Sum of microscopic kinetic energies of the system constituents and of the potential energy of mutual interaction between the constituents.

It is a function of the system state variables.

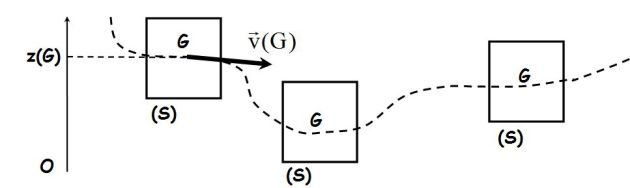
If the system (with masse \(M_{tot}\)) is in movement in (R), the mechanical energy \(E_m\) will then take into account the macroscopic kinetic energy and macroscopic gravitational potential energy :

\({E_m} = \;\;U\; +\;\frac{1}{2}{M_{tot}}v{(G)^2}\; +\;{M_{tot}}g\;z(G)\)

Where \(G\) is the center of inertia of the system.

Consider a closed and motionless thermodynamic system \((S)\) in the laboratory frame (R).

This system undergoes a transformation in which its internal energy varies :

\(\Delta U=U_f-U_i\)

This variation is due to two contributions :

• To the work \(W\) of forces (pressure, for example) that act on the system \((S)\).

• To heat transfer (amount of heat) \(Q\) received by the system \((S)\).

The first law of thermodynamics is the law of conservation of energy :

\(\Delta U = {U_f} - {U_i} = W + Q\)

For an elementary transformation (reversible or quasi-static) :

\(dU = \delta W + \delta Q\)

If the system \((S)\) is driven by an ensemble movement which respects to the laboratory frame (R) :

\(\Delta \left( {U + \frac{1}{2}{M_{tot}}v{{(G)}^2} + {M_{tot}}g\;z(g)} \right) = W + Q\)

• Pure thermal transformation (\(W = 0\)) :

  \(\Delta U=Q\)

• Adiabatic transformation (\(Q = 0\)) :

  \(\Delta U=W\)

• Cyclic transformation (suite of transformations during which the system returns to its original state) :

  \((\Delta U )_{cycle}= (W+Q)_{cycle}=0\)

A fun video : "Entropy viewed by The Shadoks"

Pour lire la vidéo, cliquer ici :

Entropy is a state function, additive and extensive.

Elementary expression of 2^nd law :

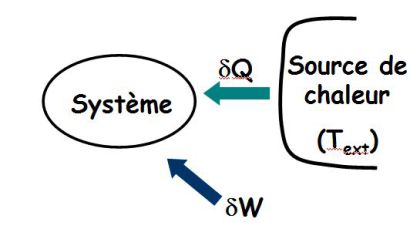
The system receives work and heat \(\delta Q\) from a heat source of temperature \(T_{ext}\).

Its variation of entropy \(dS\) verifies :

\(dS \ge \frac{{\delta Q}}{{{T_{ext}}}}\)

What is written in the form :

\(dS = \frac{{\delta Q}}{{{T_{ext}}}} + \delta {S_{creation}} = \delta {S_{exchange}} + \delta {S_{creation}}\)

With :

\(\delta {S_{exchange}} = \frac{{\delta Q}}{{{T_{ext}}}}\;\;\;\;\;and\;\;\;\;\;\delta {S_{creation}} \ge 0\)

• \(\delta S_{exchange}\) : entropy of exchange depends on the heat exchange with the outside ; its sign is arbitrary.

• \(\delta S_{creation}\) : the entropy of creation (positive or zero, only in the case of a reversible transformation) is related to the internal transformation within the system and characterizes the degree of irreversibility of the transformation (heterogeneity of temperature, concentrations, pressure disequilibrium, ...).

Expression of the 2^nd principle to a finite transformation :

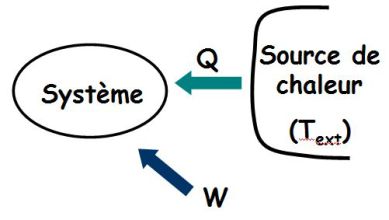
The system receives work and heat from a heat source of temperature \(T_{ext}\).

Its entropy variation \(\Delta S\) verifies :

\(\Delta S \ge \int_{EI}^{EF} {\frac{{\delta Q}}{{{T_{ext}}}}}\)

What is written in the form :

\(\Delta S = \int_{EI}^{EF} {\frac{{\delta Q}}{{{T_{ext}}}}} + {S_{creation}} = {S_{exchange}} + {S_{creation}}\)

With :

\({S_{exchange}} = \int_{EI}^{EF} {\frac{{\delta Q}}{{{T_{ext}}}}} \;\;\;\;\;and\;\;\;\;\;{S_{creation}} \ge 0\)

• In variables \(T\) and \(V\) (for \(n\) moles) :

  \(S(T,V) = n\frac{1}{{\gamma - 1}}R\ln (T) + nR\ln (V)\; + cste\)

• In variables \(T\) and \(P\) (for \(n\) moles) :

  \(S(T,P) = n\frac{\gamma}{{\gamma - 1}}R\ln (T) - nR\ln (P)\; + cste\)

  With :

  \(\gamma = \frac {C_P}{C_V}\).