Fluid Mechanics

We can illustrate the terms of divergence and curl for some types fields : (see figure below and the lesson Vector calculus)

The divergence and the curl are zero for the field whose field lines are parallel.

The divergence is negative for fields whose field lines converge to a point. It is positive for a diverging field.

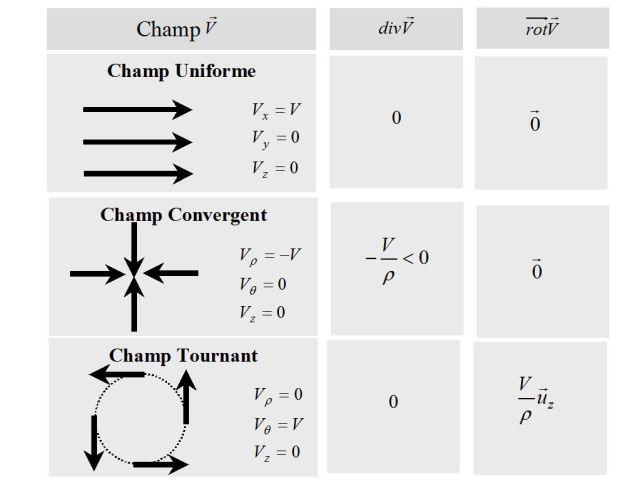
The curl operator of the last field (fields lines rotate around point O in the positive side) is positive.

The considered field can be that of velocity of a solid rotating about the(Oz) axis .

The speed of a point of the solid is, if \(\vec \Omega=\Omega \vec u_z\) denotes the rotation vector of the solid, \(\vec v(M) = \vec \Omega \wedge \overrightarrow {OM}\).

Using Cartesian coordinates :

\(\overrightarrow {rot}\; \vec v = 2\vec \Omega\)

This result allows to associate the curl operator to the idea of rotation.