Fluid Mechanics

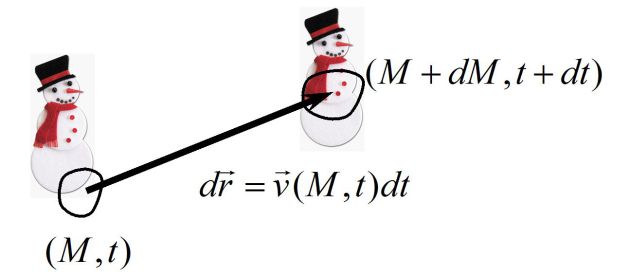
Imagine a little boy (or a snowman) on a fluid particle (always the same) : changes in the quantities it measures (speed, pressure, density, ...) are the variations of particle, that is to say, the variations in sizes related to the same particle that moves over time.

We intuitively understand that to study the motion of a fluid particle subject to different forces, we have to determine its acceleration.

But how to calculate the acceleration of a fluid particle by using Eulerian formalism ?

The differential of the velocity of a fluid particle (always the same) is equal to :

\(d\vec v = \frac{{\partial \vec v}}{{\partial t}}dt + \frac{{\partial \vec v}}{{\partial x}}\;dx + \frac{{\partial \vec v}}{{\partial y}}\;dy + \frac{{\partial \vec v}}{{\partial z}}\;dz\)

During the time interval \(dt\), the fluid particle has moved :

\(d\vec r=\vec v dt\)

Where :

\(d\vec v = \frac{{\partial \vec v}}{{\partial t}}dt + \frac{{\partial \vec v}}{{\partial x}}\;v_x \;dt + \frac{{\partial \vec v}}{{\partial y}}\;v_y \;dt + \frac{{\partial \vec v}}{{\partial z}}\;v_z\; dt\)

And the particle acceleration can be written as :

\(\vec a = \frac{{d\vec v}}{{dt}} = \frac{{\partial \vec v}}{{\partial t}} + v_x \;\frac{{\partial \vec v}}{{\partial x}} + v_y \;\frac{{\partial \vec v}}{{\partial y}} + v_z \;\frac{{\partial \vec v}}{{\partial z}}\)

Or again :

\(\vec a = \frac{{d\vec v}}{{dt}} = \frac{{\partial \vec v}}{{\partial t}} + (\vec v.\overrightarrow {grad} )\;\vec v\)

Strictly speaking, \(\vec v\) in the left term is the velocity of the fluid particle (and \(d/dt\) is called particle derivative, \(D/Dt\) is still denoted) whereas in other term, \(\vec v\) denotes the velocity field throughout the fluid.

Finally, the term \((\vec v.\overrightarrow {grad} )\;\vec v\) can realize that, even in a steady flow (in the Eulerian sense), the spatial variations of the speed corresponding acceleration for the particles.