Capacitors
Définition : Definition of a capacitor
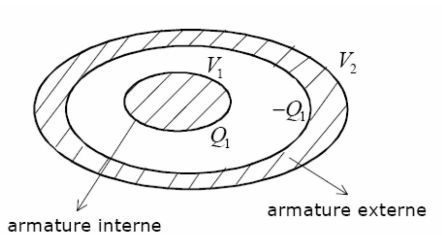
A set of two conductors, one of which is empty and surrounds the other completely is called a capacitor.
The space which separates the two frames can either be empty or filled with an insulator (“dielectric”).
The facing frames carry opposite charges, noted \(Q_1\) and \(-Q_1\).
The capacitance of the capacitor is defined by :
\(C=\frac{Q_1}{V_1-V_2}\)
Fondamental : Energetic aspect, plane capacitor example
In electricity, we have seen that the energy of a capacitor could be written as such :
\(E_c=\frac{1}{2}Cu^2\)
\(u\) is the voltage difference between the terminals of the capacitor.
For a plane capacitor, the electric field inside the conductive plates is even and is equal to :
\(E=\frac {\sigma}{\varepsilon_0}=\frac{q}{S\varepsilon_0}\)
Where \(q\) is the charge of the positive plate and \(S\) its surface.
The tension \(u\) is obtained by the line integral around a loop of the field between the two conductive plates :
\(u=dE=\frac{qe}{S\varepsilon_0}\)
By calling \(e\) the distance between the two plates.
Thus we find the capacitance of a plane capacitor :
\(C=\frac{q}{u}=\frac{\varepsilon_0 S}{e}\)
We can also see that the energy of a capacitor can be written as such :
\(E_c=\frac{1}{2}Cu^2=\frac{1}{2}\frac{\varepsilon_0 S}{e} ({\frac{qe}{S\varepsilon_0}})^2\)
Thus :
\(E_c=\frac{1}{2}\varepsilon_0 E^2 (Se)\)
By noticing that \(eS\) represents the volume between the two frames, the expression of the density of purely electric energy (the electric energy per unit of volume) is :
\(e_e=\frac{1}{2}\varepsilon_0 E^2 \)
The expression of this energy is specified in the lesson about electromagnetic energy review.
Exemple : Calculation of the capacitance

Gauss' law applied to a sphere of center O and radius \(r\) leads to :
\(\vec E = \frac{Q_1}{4\pi \varepsilon_0 r^2} \vec e_r\)
To determine the voltage difference between the two frames, let's calculate the line integral of the electric field between the two frames :
\(V_1-V_2=\int_a^b\frac{Q_1}{4\pi \varepsilon_0 r^2} dr=\frac{Q_1}{4\pi \varepsilon_0 }(\frac{1}{a}-\frac{1}{b})\)
Where \(a\) and \(b\) are the radius of the two electrodes (\(b>a\)).
Hence we can deduce the capacitance of the spherical capacitor :
\(C=4\pi \varepsilon_0 \frac{ab}{b-a}\)
Cylindrical capacitor :
The method used is identical to the one used for the spherical capacitor
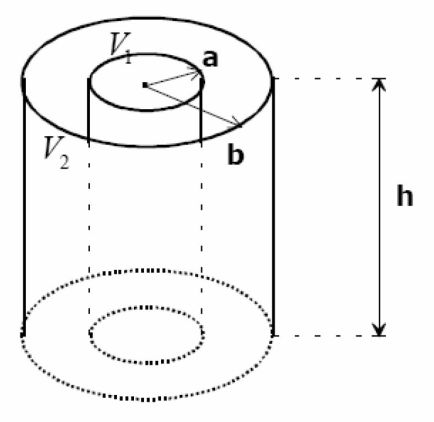
The electric field between the two frames is given by Gauss' Law :
\(\vec E = \frac {Q_1}{2\pi \varepsilon_0 h r} \vec e_r\)
Let's compute the line integral of the field between the two frames :
\(V_1-V_2=\int_a^b\frac {Q_1}{2\pi \varepsilon_0 h r}dr=\frac{Q_1}{2\pi \varepsilon_0 h} ln(\frac{b}{a})\)
Where \(a\) and \(b\) are the radius of the two frames (\(b>a\)).
Hence the capacitance :
\(C=\frac{2\pi \varepsilon_0 h}{ln(b/a)}\)