Electro-dynamic loudspeaker principle
Fondamental : Mechanic and electric equations of the loudspeaker
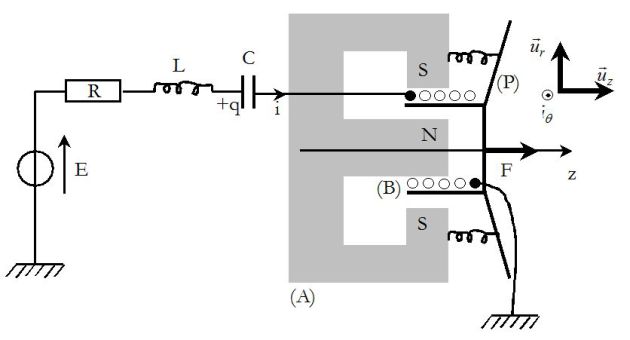
The following figure represents a device used as a speaker or microphone.
\((A)\) is a permanent magnet of revolution symmetry around \((Oz)\) axis.
In the air gap is a radial magnetic field.
In the area where the coil \((B)\) moves, attached to the pavilion \((P)\), the magnetic field is written :
\(\vec B = B \;\vec u_r\)
\((P)\) is a system of mass \(m\), likely to move along \((Oz)\) axis.
It can be set in translation movement if it is subject to an exterior force \(F\vec u_z\).
It is also subject to dissipative forces of sum \(-h\dot z \;\vec u_z\), spring forces of sum \(-kz\;\vec u_z\) applied by a system of springs, as well as Laplace's forces of sum \(\vec f\) applied on \((B)\).
The pavilion has a total length of wire equal to \(\ell\) and carries an intensity \(i\).
It is admitted, by neglecting the helicity of \((B)\), that each element of the wire can be represented in cylindrical coordinates by :
\(d\vec \ell = d\ell \vec u_{\theta}\)
\((B)\) is powered by a voltage source \(E\) through the circuit.
\(R\), \(L\) and \(C\) are the total resistance, inductance and capacitance, relatively to the whole of the circuit, \((B)\) included.
\(\vec f\) can be expressed as a function of \(i=\dot q\), \(B\) and \(\ell\).
Indeed, if we sum Laplace's forces on several elements of \((B)\) :
\(d\vec f = i\;d\ell \;{\vec u_\theta } \wedge B\;{\vec u_r} = - iBd\ell \;{\vec u_z}\;\;\;\;\;\;\;and\;\;\;\;\;\;\;\vec f = - iB\ell \;{\vec u_z}\)
The inertia center theorem applied to the pavilion \((P)\) and projected on \((Oz)\) axis gives the differential equation (M) verified by \(z(t)\).
It shows the mechanical behavior of the system :
\(m\ddot z = - h\dot z - kz - B\ell i + F\;\;\;\;\;\;\;so\;\;\;\;\;\;\;m\ddot z + h\dot z + kz = - B\ell i + F\)
The mechanic equation (M) of the system is obtained.
In order to obtain the electric equation, \(B\), \(\ell\) and the induced electromotive force \(e\) in \((B)\) must be expressed as functions of \(v=\dot z\).
The electromotive force is induced on an element \(d\vec \ell\) of \((B)\) :
\(de = (\vec v \wedge \vec B).d\vec \ell = (\dot z\;{\vec u_z} \wedge B\;{\vec u_r}).d\ell \;{\vec u_\theta } = B\dot z\;d\ell\)
After integration along \((B)\) in the positive direction of \(i\) :
\(e = B\dot z\ell = B\ell v\)
(We also can obtain this expression for \(e\) using an analogy with the Laplace rails).
Kirchhoff's law gives the electric equation (E) of the circuit :
\(e = B\dot z\ell = B\ell v\)
Fondamental : Energy review
Let's compute \((M).v+(E).i\) :
\((m\ddot z + h\dot z + kz).v + (L\ddot q + R\dot q + \frac{1}{C}q).i = ( - B\ell i + F).v + (B\ell v + E).i\)
This equation can be written as such :
\(\frac{{dU}}{{dt}} = Fv + Ei - R{i^2} - h{v^2}\)
With :
\(U = \frac{1}{2}m{v^2} + \frac{1}{2}k{z^2} + \frac{1}{2}L{i^2} + \frac{1}{2}\frac{{{q^2}}}{C}\)
\(U\) represents the mechanic energy of the system and its electromagnetic energy.
The previous equation expresses the energy conservation :
The derivative of \(U\) is equal to the sum of powers provided by the two energy sources of the system : the exterior force and the voltage source .
To this is subtracted the power dissipated via friction forces (or acoustic energy when the speaker emits a noise) or Joule effect.
Méthode : Study in forced sinusoidal regime
The system is now under a sinusoidal steady state at fixed frequency.
The equations (M') and (E') linking the complex representations of \(v\), \(I\), \(F\) and \(E\) can be written as such :
\(m\ddot z + h\dot z + kz = - B\ell i + F\;\;\;\;\;\;\;gives\;\;\;\;\;\;\;\underline \xi \;\underline v = - B\ell \;\underline i + \underline F \;\;\;\;\;\;\;(M')\)
And :
\(L\ddot q + R\dot q + \frac{1}{C}q = B\ell v + E\;\;\;\;\;\;\;gives\;\;\;\;\;\;\;\underline z \;\underline i = B\ell \underline v + \underline E \;\;\;\;\;(E')\)
The complex notation in \(exp(j\omega t)\) has been introduced and :
\(\underline z = R + j\left( {L\omega - \frac{1}{{C\omega }}} \right)\;\;\;\;\;\;\;and\;\;\;\;\;\;\;\underline \xi = h + j\left( {m\omega - \frac{k}{\omega }} \right)\)
\(\underline z\) is the complex impedance of the \(RLC\) series dipole.
\(\underline \xi \) is the mechanic impedance of the mobile pavilion (ratio between Laplace's force and speed).
When it is used as a speaker, \(F\) is equal to zero, the energy of the system comes from the source of voltage \(E\).
The answer to the system is characterized by relations \(v(i)\) and \(i(E)\), given by (E') and (M') :
\(\underline \xi \;\underline v = - B\ell \;\underline i \;\;\;\;\;\;\;and\;\;\;\;\;\;\;\underline z \;\underline i = B\ell \;\underline v + E\)
Hence :
\(\underline v = - \frac{{B\ell }}{{\underline \xi }}\;\underline i \;\;\;\;\;\;\;and\;\;\;\;\;\;\;\underline i = \frac{{\underline E }}{{\underline z + \underline Z }}\)
The quantity \(\underline Z\) is introduced :
\(\underline Z = \frac{{{B^2}{\ell ^2}}}{{\underline \xi }}\)
From an electro kinetic point of view, it is as though, because of the movement in the magnetic field, another electric impedance \(\underline z\) is added to \(\underline Z\).
This impedance, called motion impedance, characterizes the electro-mechanic coupling done by the assemblage.
If the frequency \(\nu = \frac{\omega }{{2\pi }}\) is included in \(\left[ {20\;Hz,20\;kHz} \right]\), the vibrations of the pavilion will create an acoustic pressure wave which will generate audible sound.
When it is used as a microphone, then \(E\) is equal to zero.
The energy of the system comes from the sinusoidal force \(F\) which expresses the action of the pressure forces from a sound wave on \((P)\).
The answer of the system is then characterized by the function \(i(F)\) :
\(\underline i = \frac{{B\ell }}{{\underline \xi (\underline z + \underline Z )}}\underline F\)
The intensity is proportional to the applied force : the electric signal received is faithful to the force.
It will be recorded, treated and reproduced by another speaker.