The Laplace rails
Fondamental :
The bar \((AB)\), of length \(a\) and mass \(m\), has its center of mass in abscissa \(x(t)\) and its speed is \(\vec v=v(t)\vec u_x\) (with \(v(t)=\dot x(t)\)).
It is thrown with an initial speed \(v_0\) on metallic rails and it slides without friction forces.
The bar and rails form a rectangular circuit of total resistance \(R\) and of negligible inductance \(L\).
At time \(t\), its surface is \(S(t)=ax(t)\).
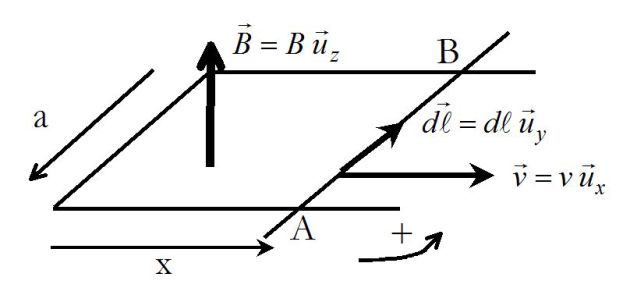
The circuit \((C)\) is placed in a permanent magnetic field \(\vec B=B\vec u_z\) created by a source exterior to \((C)\).
We want to determine the electromotive force \(e\) induced and the speed of the bar.
Méthode : Electromotive force induced determination
Faraday's law is used.
During the time \(dt\), the variation of magnetic flux is :
\(d\Phi = Ba\;dx = Bav\;dt\)
The electromotive force induced is :
\(e = - \frac{{d\Phi }}{{dt}} = - Bav\)
The circuit can be modeled by :
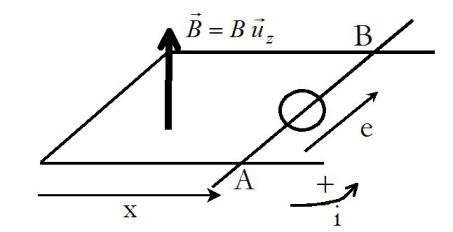
The intensity crossing the circuit can be calculated by Pouillet's law :
\(e = Ri\;\;\;\;\;\;\;so\;\;\;\;\;\;\;i = - \frac{{Bav}}{R}\) (electric equation (E))
Hence, for \(v>0\), \(i<0\) : this result could have been predicted by Lenz's law.
In fact, when the bar moves towards the right the inductive positive flux increases.
Consequently the induced flux must be negative, which corresponds to a negative induced current.
Méthode : Velocity v(t)
The bar is horizontally subject to Laplace's Force :
\(\vec F = i\;a\;{\vec u_y} \wedge B\;{\vec u_z} = iaB\;{\vec u_x} = F\;{\vec u_x}\)
Hence, for \(i<0\), \(F<0\) : this result could have been predicted by Lenz's law.
In fact the appearance of a negative braking force is a moderating effect which tends to oppose the setting in motion of the bar.
Mass center theorem applied to the bar gives : (mechanic equation (M))
\(m\frac{{dv}}{{dt}} = iaB = - \frac{{{B^2}{a^2}}}{R}v\;\;\;\;\;\;\;so\;\;\;\;\;\;\;\frac{{dv}}{{dt}} = - \frac{{{B^2}{a^2}}}{{mR}}v\)
It can be noticed that the term \(B^2a^2/R\) plays the same role as a fluid friction coefficient.
Let's write :
\(\tau = \frac{{mR}}{{{B^2}{a^2}}}\)
The characteristic period of the transitory regime, so :
\(v = v_0 \;exp(-t/\tau)\)
For the values :
\(a=10cm\) ; \(B=0,1T\) ; \(m=10g\) ; \(R=0,1\Omega\), the result is \(\tau\) = 10 s.
Fondamental : Energy aspect (example of a transducer)
The electric (E) and mechanic (M) equations of the circuit are :
\((E)\;:\;e = Ri = - Bav\;\;\;\;\;and\;\;\;\;\;(M)\;:\;m\frac{{dv}}{{dt}} = F = iaB\)
In order to have the power, we multiply (E) by \(i\) and (M) by \(v\) :
\(ei = R{i^2} = - Bav\;i\;\;\;\;\;and\;\;\;\;\;mv\frac{{dv}}{{dt}} = Fv = iaBv\)
Let's call :
\({E_c} = \frac{1}{2}m{v^2}\)
The kinetic energy of the bar, so :
\(\frac{{d{E_c}}}{{dt}} = - R{i^2}\)
The kinetic energy lost by the bar is entirely found in the form of Joule effect in the resistor.
The bar has a role of converter of mechanic energy into electric energy, which is then dissipated into heat via Joule effect.
Another situation can be studied : the bar is initially still and all along the circuit is introduced a voltage difference (a battery for example), which creates intensity.
The bar is then set in motion, because of the Laplace's forces.
The same system has the role of receiver by converting electric energy into mechanic energy.
It is the principle of an electric engine.
More generally, a system which is likely to transform mechanic energy into electric energy or vice versa is called an “electro-mechanic transducer”.
Complément : Application of Lenz's law to Foucault's currents
According to a principle similar to the previous circuit, Foucault's induced currents in massive and mobile conductors in permanent magnetic fields are the origin of Laplace's forces.
These forces tend to oppose the movement which gave them birth.
This is the principle of electromagnetic braking, commonly used for haulers and high speed trains.
