Laplace's force
Fondamental : Case of parallelepiped conductor
This lesson uses the same notations as the lesson about Hall effect.
The following video shows the Laplace's force experimentally (Alain Le Rille, CPGE teacher at lycee Janson de Sailly, Paris)
What is the expression of the force applied by the magnetic field \(\vec B\) to the conductor ?
The set of carrier electrons and metallic cations in the conductor is subject to the following forces due to the magnetic field \(\vec B\) :
On the carrier electrons :
\(n(abL)\;\left[ { -e\vec E_e - e{{\vec E}_H} + - e\vec v \wedge \vec B} \right]\)
Where \(n\) is the density of charge carriers.
On metallic cations (still) :
\(n(abL)\;\left[ {e\vec E_e +e{{\vec E}_H}} \right]\)
Globally the conductor is subject to the force :
\({\vec F_L} = n(abL)\;\left[ { - e\vec v \wedge \vec B} \right]\)
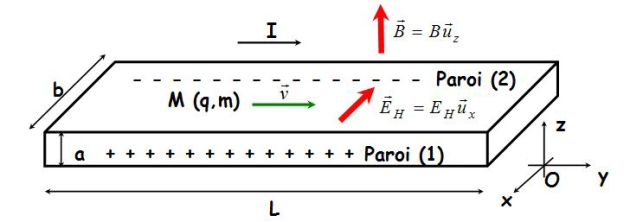
The intensity \(I\) can be expressed as:
\(I = jab = - nevab\)
So :
\({\vec F_L} = IL\;{\vec u_y} \wedge \vec B = I\;\vec L \wedge \vec B\)
Attention : Laplace's force for a thread-like conductor
A portion of the thread-like circuit is travelled by the intensity \(I\) and put in a certain magnetic field \(\vec B\).

The conductor is subject to the force called Laplace's force :
\(d{\vec F_L} = I\;d\vec \ell \wedge \vec B\)
By writing :
\(I = js\;\;\;so\;\;\;I\;d\vec \ell = js\;d\vec \ell = \vec j\;s\;d\ell = \vec j\;d\tau\)
Then :
\(d{\vec F_L} = \vec j\;d\tau \wedge \vec B\)
This is the expression of the Laplace's force for volume currents.
Differences between Laplace's and Lorentz's forces :
Lorentz's force is microscopic. It is applied to charge \(q\) moving carriers in a magnetic field :
\(\vec f = q(\vec v \wedge \vec B)\)
Laplace's force is macroscopic. It is applied to any conductor, electrons and cations included.
