Raccordement d'écoulements visqueux
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
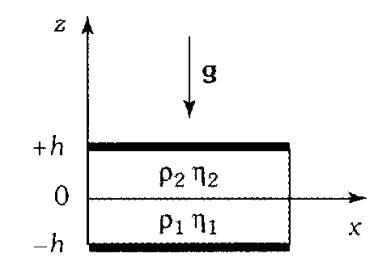
Deux fluides non miscibles s'écoulent avec un champ de vitesse \(\vec v = v(x,z)\vec u_x\) entre deux parois fixes confondues avec les plans \(z=-h\) et \(z=h\) : le fluide (1), de masse volumique \(\rho_1\) et de viscosité \(\eta_1\) s'écoule entre les plans \(z=-h\) et \(z=0\) ; le fluide (2), de masse volumique \(\rho_2\) et de viscosité \(\eta_2\) s'écoule entre les plans \(z=0\) et \(z=h\) (voir figure ci-dessous).
Les deux fluides sont en contact dans le plan \(z=0\).
Question
1) Que dire du rapport \(\rho_2 / \rho_1\) ?
Solution
L'énergie potentielle des deux fluides doit être minimale : le fluide le plus dense est en bas et donc \(\rho_2 / \rho_1<1\).
Question
2) Justifier que \(v(x,z)\) ne dépend pas de \(x\). En déduire la valeur de l'accélération des particules fluides.
Solution
L'écoulement étant incompressible, \(div \vec v =0\). Par conséquent, \(\frac{{\partial {\rm{v}}}}{{\partial {\rm{x}}}}=0\).
La vitesse ne dépend pas de \(x\).
L'accélération convective est nulle ainsi que \(\frac{{\partial {\rm{v}}}}{{\partial {\rm{t}}}}\) (régime stationnaire).
Question
3) Montrer que :
\(P(x,z>0)+\rho_2 gz=P(x,z<0)+\rho_1 gz=\Phi (x)\)
Où \(\Phi(x)\) est une fonction inconnue de la seule variable \(x\).
Solution
L'équation de Navier - Stokes donne, pour les deux fluides :
\(- \overrightarrow {grad} P + \eta \Delta \vec v + \mu \vec g = \vec 0\)
En projetant sur (Oz) :
\(\frac{{\partial P}}{{\partial z}} = - \rho g\)
En intégrant pour le fluide (1) puis (2) :
\(P(x,z < 0) = - \rho _1 gz + \phi _1 (x)\;\;\;\;\;;\;\;\;\;\;P(x,z > 0) = - \rho _2 gz + \phi _2 (x)\)
La pression est continue à 'interface en \(z=0\). Par conséquent, \( \phi _1 (x) = \phi _2 (x) = \phi (x)\).
Ainsi :
\(P(x,z>0)+\rho_2 gz=P(x,z<0)+\rho_1 gz=\Phi (x)\)
Question
4) On donne :
\(P(x=0,z=0)-P(x=L,z=0)=\Delta P\)
Montrer que \(\frac{{\partial {\rm{P}}}}{{\partial {\rm{x}}}}(x,z)\) est une constante et déterminer la forme générale du champ des vitesses dans chacun des fluides.
Solution
En projetant l'équation de Navier – Stockes sur (Ox) :
\(- \frac{{\partial P}}{{\partial x}} + \eta _1 \frac{{\partial ^2 v}}{{\partial z^2 }} = 0\;\;\;\;\;\;(pour\;z < 0)\)
\(\frac{{\partial P}}{{\partial x}} = \frac{{d\phi (x)}}{{dx}} = \eta _1 \frac{{d^2 v}}{{dz^2 }} = cste = C\)
(En effet, le terme de gauche ne dépend que de x et celui de droite ne dépend que de z).
Par intégration :
\(\phi (L) - \phi (0) = CL\;\;\;\;\;soit\;\;\;\;\;C = - \frac{{\Delta P}}{L}\)
On en déduit ensuite :
\(v(z < 0) = - \frac{{\Delta P}}{{2\eta _1 L}}z^2 + \alpha _1 z + \beta _1 \;\;\;\;\;;\;\;\;\;\;v(z > 0) = - \frac{{\Delta P}}{{2\eta _2 L}}z^2 + \alpha _2 z + \beta _2\)
Question
5) Quelles sont les conditions aux limites permettant d'achever la détermination du champ des vitesses ?
On ne demande pas de mener les calculs.
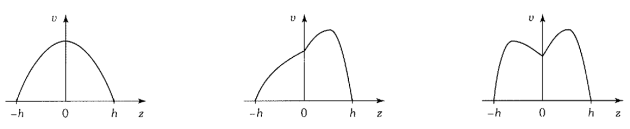
Parmi les profils de vitesse proposés sur les figures ci-après, quel est le seul profil susceptible de convenir ?
Solution
Les vitesses doivent être nulles en \(z=-h\) et \(z=h\) et continues en z = 0.
Cette dernière condition donne \(\beta_1=\beta_2\).
La 4ème relation est obtenue en étudiant les forces qui s'appliquent sur un élément de surface dS entre les deux fluides. Le fluide (1) exerce la force :
\(d\vec F_1 = - \eta _1 \left( {\frac{{\partial v}}{{\partial z}}} \right)_{0^ + } dS\vec u_x = - \alpha _1 \eta _1 dS\vec u_x\)
De même :
\(d\vec F_2 = - \eta _2 \left( {\frac{{\partial v}}{{\partial z}}} \right)_{0^ - } dS\vec u_x = - \alpha _2 \eta _2 dS\vec u_x\)
La condition \(d\vec F_1 + d\vec F_2 = \vec 0\) donne \(\alpha _1 \eta _1 = \alpha _2 \eta _2\).
On voit donc que \( \frac{{\partial v}}{{\partial z}}\) est discontinue en \(z=0\).
Le profil (a) n'est donc pas le bon !
La dérivée \( \frac{{\partial v}}{{\partial z}}\) ne change pas de signe en \(z=0\). Le profil satisfaisant est donc le (b).