Mesure interférentielle de la bande passante d'un filtre
(20 minutes de préparation)
Un interféromètre de Michelson est monté en coin d'air et est éclairé par une source de lumière blanche étendue.
On intercale un filtre jaune laissant passer la lumière au voisinage de λ = 580 nm et de bande passante Δλ.
On projette la figure d'interférences obtenues sur un écran.
On translate un des miroirs à vitesse v = 1,0 \(\mu\)m.s-1 constante et on enregistre l'éclairement E(t) au centre de la figure d'interférences.
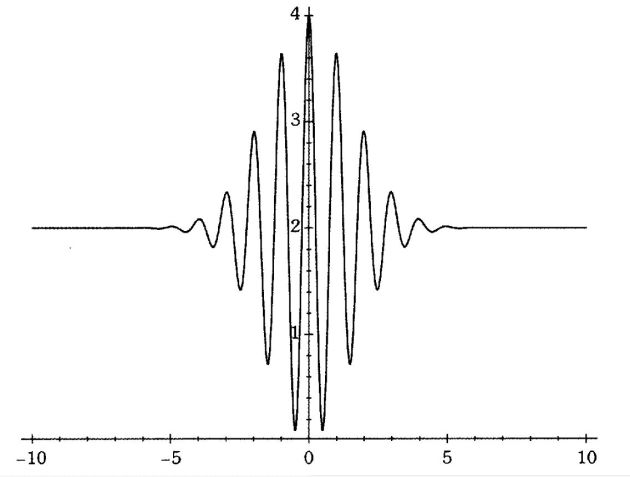
On obtient le graphe ci-contre où l'unité de temps en abscisse est la seconde.
Question
En déduire une mesure approchée de la longueur de cohérence L* de la source de lumière jaune équivalente à la source blanche munie du filtre jaune.
Solution
On note \(t_1=-4s\) et \(t_2=4s\) les instants où il y a brouillage, soit une durée \(\Delta t=t_2-t_1=8s\).
Lorsqu'il y a brouillage, la différence de marche (égale à deux fois la distance entre les miroirs) est égale à la longueur de cohérence \(L^*\).
Ainsi :
\(L^*=2v(-t_1)=2vt_2\)
Donc :
\(L^*=v\Delta t=8\mu m\)
Question
En déduire une valeur approchée de la bande passante Δλ du filtre.
Solution
On sait que le temps de cohérence \(\tau_c\) et la bande passante \(\Delta \nu\) d'un filtre sont reliés par :
\(\tau_c \Delta \nu \approx 1\)
Or :
\(\lambda = \frac{c}{\nu }\;\;\;donc\;\;\;\Delta \nu = \frac{c}{{{\lambda ^2}}}\Delta \lambda\)
Et :
\(L^*=c\tau_c\)
D'où :
\(\frac{c}{{{\lambda ^2}}}\Delta \lambda \frac{{{L^*}}}{c} = \frac{{\Delta \lambda }}{{{\lambda ^2}}}{L^*} \approx 1\;\;\;soit\;\;\;\;\Delta \lambda \approx \frac{{{\lambda ^2}}}{{{L^*}}}\)
L'application numérique donne \(\Delta \lambda=42nm\).
Cet ordre de grandeur est très supérieur à la valeur \(\Delta \lambda\approx 0,1 nm\) valable pour les raies émises par les lampes spectrales polychromatiques utilisées en travaux pratiques.