Interféromètre de Twyman
(20 minutes de préparation)
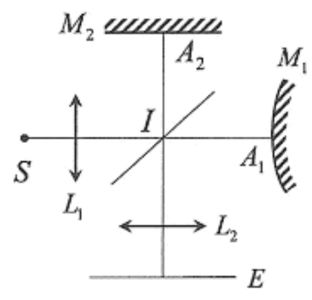
Le dispositif est un interféromètre de Michelson où le miroir M1 est un miroir sphérique convexe de grand rayon R ; le miroir M2 reste plan et au début :
\(IA_1=IA_2\)
La source S, placée au foyer objet de L1, est peu étendue. Elle est monochromatique de longueur d'onde λ.
Question
Quel type de franges observe-t-on ? Où sont-elles localisées ? Quel est le rôle de la lentille L2 ?
Solution
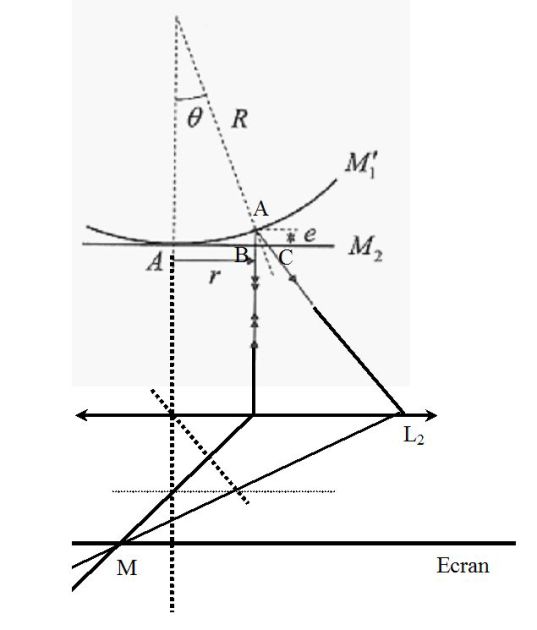
On utilise le schéma équivalent du Michelson (voir figure). Le miroir sphérique est remplacé par son symétrique M'1 par rapport à la séparatrice.
Un rayon arrive sous incidence normale sur le miroir M2 et repart vers le bas ; un rayon semblable se réfléchit sur le miroir M'1 selon les lois de la réflexion. Les interférences sont localisées sur les miroirs.
La lentille L2 sert à former l'image des miroirs (et des franges) sur un écran.
La différence de marche entre les deux rayons arrivant au point M est :
\(\delta = \left[ {(BA) + (ACM)} \right] - (BM) = (BA) + (ACM) - (ABM) + (AB)\)
Or, par stigmatisme :
\((ABM)=(ACM)\)
Donc :
\(\delta =2(AB)=2e\)
Or :
\(e = R(1 - \cos \theta ) \approx R\frac{{\theta ^2 }}{2} \approx R\frac{1}{2}\left( {\frac{r}{R}} \right)^2 \approx \frac{{r^2 }}{{2R}}\)
Donc :
\(\delta = \frac{{r^2 }}{R}\)
Question
Déterminer le rayon rk de la kième frange brillante.
Solution
Les franges lumineuses sont des anneaux (anneaux de Newton), dont les rayons sont donnés par :
\(\delta _k = \frac{{r_k^2 }}{R} = k\lambda _0\)
Soit :
\(r_k = \sqrt {kR\lambda _0 }\)
Pour obtenir les rayons vus à l'écran, il faut prendre en compte le grandissement dû à la lentille.