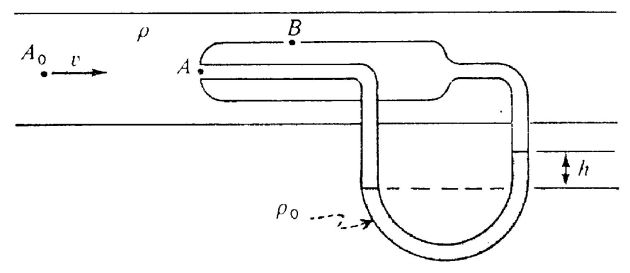
Tube de Pitot double
Consacrer 10 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère l'écoulement permanent d'un gaz dans une conduite cylindrique munie d'un tube de Pitot double.
Soit ρ la masse volumique du gaz, ρ0 la masse volumique du liquide remplissant le tube en U.
On admettra que la vitesse v du gaz a la même valeur en tout point d'une section droite de la conduite.
Question
Exprimer la vitesse v puis le débit volumique Dv de la conduite en fonction de ρ0, ρ, g, h et de la section droite S de la conduite.
Indice
Reprendre la méthode vue dans la vidéo. Noter que les deux masses volumiques \(\rho\) et \(\rho_0\) sont du même ordre de grandeur.
Solution
On néglige la dénivellation entre A et B. La relation de Bernoulli entre A0 et A donne : (A est un point d'arrêt)
\(P_{A_0 } + \frac{1}{2}\rho v^2 = P_A\)
De même, entre B0 et B (mêmes altitudes et vitesses) :
\(P_{B_0}=P_B\)
On en déduit :
\(P_A - P_B = P_{A_0 } + \frac{1}{2}\rho v^2 - P_{B_0 }\)
Loin du tube, le théorème de Bernoulli donne :
\(P_{A_0 } = P_{B_0 }\)
Finalement :
\(P_A - P_B = \frac{1}{2}\rho v^2\)
Dans le tube en U, on peut écrire :
\(P_A + \rho g(h' + h) = P_B + \rho gh' + \rho _0 gh\)
Soit :
\(P_A - P_B = (\rho _0 - \rho )gh = \frac{1}{2}\rho v^2\)
Finalement :
\(v = \sqrt {\frac{{2(\rho _0 - \rho )}}{\rho }gh} \;\;\;\;\;\;\;\;et\;\;\;\;\;\;\;\;D_v = Sv = Sv = S\sqrt {\frac{{2(\rho _0 - \rho )}}{\rho }gh}\)