Vidange d'une clepsydre
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
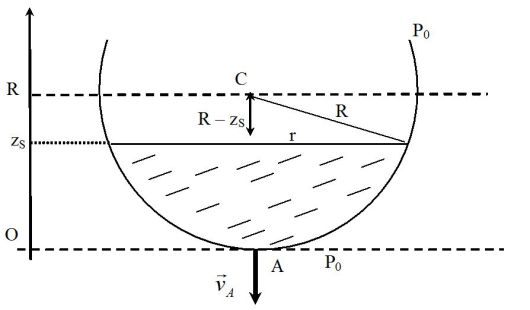
Un réservoir de forme sphérique, de rayon R = 40 cm, est initialement rempli à moitié d'eau de masse volumique ρ = 103 kg.m– 3.
La pression atmosphérique P0 règne au-dessus de la surface libre de l'eau grâce à une ouverture pratiquée au sommet S du réservoir.
On ouvre à t = 0 un orifice A circulaire de faible section s = 1 cm2 au fond du réservoir.
Question
Établir l'équation différentielle en zs(t), si zs(t) est la hauteur d'eau dans le réservoir comptée à partir de A, à l'instant t.
Indice
Utiliser la formule de Torricelli. Écrire r en fonction de z.
Solution
En négligeant la vitesse de la surface libre de l'eau, le théorème de Bernoulli entre la surface et la sortie A donne :
\(P_0 + \mu gz = P_0 + \frac{1}{2}\mu v_A^2\)
D'où :
\(v_A = \sqrt {2gz_S }\)
On retrouve la formule de Torricelli.
L'eau étant incompressible, le débit volumique se conserve :
\(sv_A = - \pi r^2 \frac{{dz_S }}{{dt}}\)
Or :
\(r^2 = R^2 - (R - z_S )^2 = z_S (2R - z_S )\)
Soit, après avoir séparé les variables :
\((2R - z_S )\sqrt {z_S } \;dz_S = - \frac{{s\sqrt {2g} }}{\pi }\;dt\)

Question
Exprimer littéralement, puis calculer, la durée TS de vidange de ce réservoir.
Solution
La durée de vidange TS est :
\(T_S = - \frac{\pi }{{s\sqrt {2g} }}\int_R^0 {(2Rz_S ^{1/2} - z_S ^{3/2} )dz_S }\)
Soit :
\(T_S = \frac{{7\pi R^2 }}{{15s}}\sqrt {\frac{{2R}}{g}}\)
L'application numérique donne 11 minutes et 10 secondes.
Question
Clepsydre :
Soit un récipient (R0) à symétrie de révolution autour de l'axe Oz, de méridienne d'équation
\(r=az^n\)
Où r est le rayon du réservoir aux points de cote z comptée à partir de l'orifice C, de faible section s = 1 cm2 percé au fond du réservoir.
Déterminer les coefficients constants n et a, donc la forme de (R0), pour que le cote du niveau d'eau placée dans (R0) baisse régulièrement de 6 cm par minute au cours de la vidange.
Indice
Noter bien que le débit linéique \(dz/dt\) est ici une constante.
Solution
La clepsydre est caractérisée par une baisse du niveau par seconde constante :
\(k = - \frac{{dz}}{{dt}} = - 10^{ - 3} \;m.s^{ - 1}\)
On peut encore écrire :
\(v_A = \sqrt {2gz} \;\;\) et \(sv_A = - \pi r^2 \frac{{dz}}{{dt}}\)
Soit :
\(s\sqrt {2gz} = - \pi r^2 \frac{{dz}}{{dt}} = \pi r^2 k\)
Or, \(r=az^n\), donc :
\(s\sqrt {2g} \;z^{1/2} = \pi a^2 k\;z^{2n}\)
Cette relation est valable pour tout z, par conséquent n = 1 / 4. On en déduit également :
\(a = \sqrt {\frac{{s\sqrt {2g} }}{{\pi k}}} = 0,375\)
Finalement, l'équation de la méridienne est :
\(r=0,375z^{1/4}\)