Pression dans un fluide
Définition : Pression au sein d'un fluide
La pression P(M) exercée au point M par le fluide est donnée par :
\({\vec F_P} = P(M)\;S\;\vec n\)
Si la surface est élémentaire :
\(d{\vec F_P} = P(M)\;dS\;\vec n\;\;\;\;;\;\;\;\;P(M) = \frac{{d{F_P}}}{{dS}}\)

Fondamental : Équivalent volumique des forces de pression
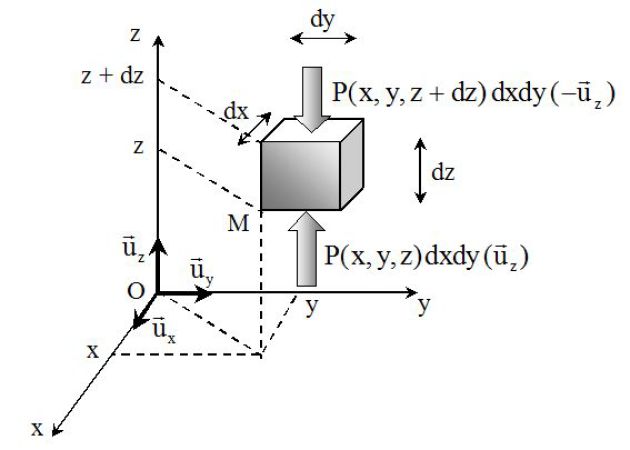
On considère une particule de fluide de forme parallélépipédique (voir figure).
La force résultante de pression qui s'exerce dans la direction (Oz) par exemple, est donnée par :
\(\begin{array}{l}d{{\vec F}_z} = - P(x,y,z + dz)\,dxdy\,{{\vec u}_z} + P(x,y,z)\,dxdy\,{{\vec u}_z} \\\;\;\;\;\;\;\;\;\;\;\;\;\;d{{\vec F}_z} = - \frac{{\partial P(x,y,z)}}{{\partial z}}\,(dxdydz)\,{{\vec u}_z} \\\end{array}\)
La force totale de pression subie par la particule de fluide peut ainsi s'écrire :
\(\begin{array}{l}d\vec F = - \left( {\frac{{\partial P(x,y,z)}}{{\partial x}}\,\,{{\vec u}_x} + \frac{{\partial P(x,y,z)}}{{\partial y}}\,\,{{\vec u}_y} + \frac{{\partial P(x,y,z)}}{{\partial z}}\,\,{{\vec u}_z}} \right)\,d\tau \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;d\vec F = - (\mathop {grad}\limits^ \to P)\,d\tau \\\end{array}\)
Ainsi, la force volumique de pression est :
\(\vec f_v = - \mathop {grad}\limits^ \to P\)