La poussée d'Archimède
Fondamental : Le principe d'Archimède
« Tout corps plongé dans un fluide subit, de la part de celui-ci, un force (poussée) dirigée vers le haut et égale au poids du volume de fluide déplacé. »
Soit :
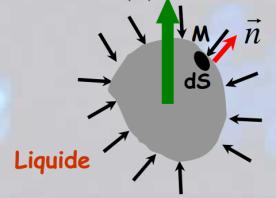
\(\vec \Pi_A=-\oiint_SP(M)\vec n dS=\mu gV\vec u_z\)
Où \(\vec n\) est le vecteur normal sortant, \(\mu\) la masse volumique du fluide et \(V\) le volume de fluide déplacé.
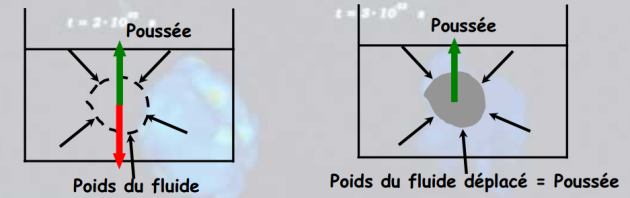
On peut proposer une démonstration "imagée" : (figure suivante)
On isole par la pensée un volume d'eau identique au volume occupé par le solide immergé.
Le volume d'eau étant en équilibre, il est soumis à une force verticale dirigée vers le haut qui compense son poids, résultant des forces de pression du fluide environnant.
On place maintenant à la place le solide immergé ayant le même volume : la poussée du reste du fluide reste et égale donc (en norme) au poids du volume de fluide déplacé.