Oscillations de deux flotteurs
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
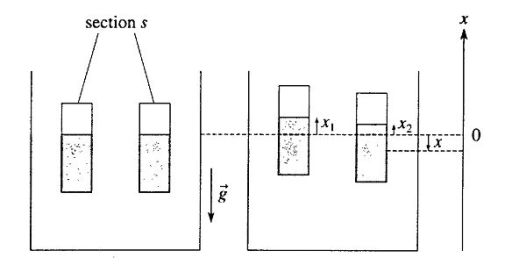
Deux flotteurs cylindriques, identiques (de section s et de masse m) peuvent osciller dans l'eau d'un récipient de section S.
Soit ρ la masse volumique de l'eau.
Les positions des flotteurs sont repérées par leurs déplacements verticaux x1 et x2 par rapport à leurs positions d'équilibre respectives.
Question
Déterminer le système d'équations différentielles qui définit le mouvement des deux flotteurs.
On admettra que la surface libre reste horizontale et que le théorème d'Archimède est applicable.
Indice
Appliquer le théorème du centre d'inertie à chaque flotteur. Penser à écrire la conservation du volume total d'eau.
Solution
Lorsque les flotteurs bougent, le niveau de l'eau dans le récipient est modifié ; on note u le déplacement algébrique de ce niveau, mesuré sur un axe vertical ascendant.
La conservation du volume total de l'eau dans le récipient conduit à l'équation :
\((x_1+x_2)s=-u(S-2s)\)
A l'équilibre, le volume immergé de chaque flotteur est :
\(V_{im}=\frac {m}{\rho}\)
On applique le théorème du centre d'inertie à chaque flotteur. En projection sur la verticale :
\(\begin{array}{l}m{{\ddot x}_1} = - mg + \rho ({V_{im}} - ({x_1} - u)s)g = - \rho ({x_1} - u)sg \\m{{\ddot x}_2} = - mg + \rho ({V_{im}} - ({x_2} - u)s)g = - \rho ({x_2} - u)sg \\\end{array}\)
En utilisant la relation donnant u, on obtient :
\(\begin{array}{l}{{\ddot x}_1} = - \omega _1^2{x_1} - \omega _2^2{x_2} \\{{\ddot x}_2} = - \omega _2^2{x_1} - \omega _1^2{x_2} \\\end{array}\)
Avec :
\(\omega _1^2 = \frac{{\rho g}}{m}\frac{{s(S - s)}}{{S - 2s}}\;\;\;\;\;et\;\;\;\;\;\omega _2^2 = \frac{{\rho g}}{m}\frac{{{s^2}}}{{S - 2s}}\)
Question
Résoudre ce système en supposant qu'à l'instant initial, les deux flotteurs sont dans leurs positions d'équilibre respectives, avec des vitesses initiales 2v0 pour le premier et v0 pour le second.
Solution
Pour découpler ces deux équations différentielles, on peut les sommer puis les soustraire.
On arrive alors à deux équations vérifiées par la somme \(\Sigma\) ou la différence D :
\(\ddot \Sigma + \Omega _1^2\Sigma = 0\;\;\;\;\;et\;\;\;\;\;\ddot D + \Omega _2^2D = 0\)
Avec :
\(\Omega _1^2 = \omega _1^2 + \omega _2^2\;\;\;\;\;et\;\;\;\;\;\Omega _2^2 = \omega _1^2 - \omega _2^2\)
En utilisant les CI, on obtient :
\({x_1} + {x_2} = \frac{{3{v_0}}}{{{\Omega _1}}}\sin ({\Omega _1}t)\;\;\;\;\;et\;\;\;\;\;{x_1} - {x_2} = \frac{{{v_0}}}{{{\Omega _2}}}\sin ({\Omega _2}t)\)
On en déduit ensuite facilement les expressions de x1 et de x2.