Téléobjectif d'appareil photo
(15 minutes de préparation)
On se propose de photographier une tour (AB) haute de 50 m et distante de \(D=2\;km\).
On assimile l'objectif standard d'un appareil photographique à une lentille mince convergente (L1) de centre O1 et de distance focale image \(f'_1 = \overline {O_1 F'_1 } = 50\,mm\).
Question
Encombrement de l'objectif standard :
Quelle serait la taille de l'image A'B' sur la pellicule si la mise au point était faite avec l'objectif standard ?
Quelle serait alors la valeur numérique de « l'encombrement » de l'objectif, c'est-à-dire la distance de l'objectif à la pellicule ?
Solution
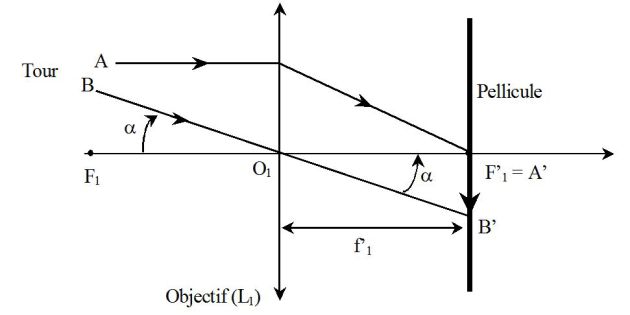
La tour peut être considérée comme un objet situé à l'infini ; par conséquent, la pellicule doit être confondue avec le plan focal image de la lentille (L1) et l'encombrement de l'appareil correspond alors à la distance focale de l'objectif, soit 50 mm.
Si \(\alpha\) désigne le diamètre apparent sous lequel le photographe voit la tour (défini par \(\alpha \approx tan(\alpha) = \overline{AB}/D\), avec \(\overline{AB}=50\;m\) et \(D=2\;km\), voir figure), alors la taille de l'image \(\overline{A'B'}\) de la tour sur la pellicule est :
\(\overline {A'B'} = - \alpha f'_1 = - (\overline {AB} /D)\,f'_1=-1,25\;mm\)
Question
Agrandissement d'un téléobjectif :
Pour agrandir l'image, on considère le système formé par la lentille convergente (L1) de distance focale \(f'_1 = \overline {O_1 F'_1 } = 50\,mm\) suivie d'une lentille divergente (L2) dont la distance focale est \(f'_2 = \overline {O_2 F'_2 } =- 25\,mm\), la distance entre les deux lentilles étant \(\overline {O_1O_2} = 31,2\;mm\).
On note \(A"B"\) l'image de la tour (AB) par le système optique des deux lentilles.
Déterminer la position de A'' par rapport à O2, puis la taille \(\overline {A"B"}\) de l'image A''B''.
Comparer cette dernière à la taille de l'image A'B' obtenue à la question précédente.
Solution
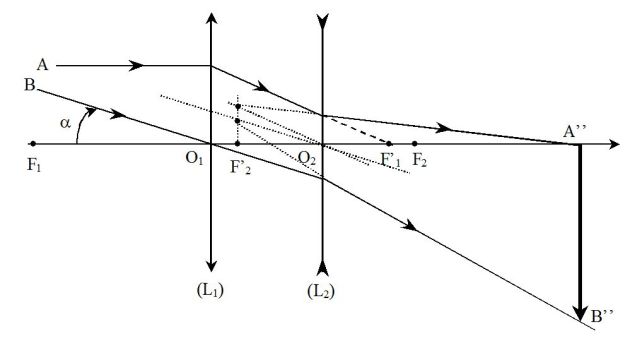
La figure suivante précise le cheminement de rayons lumineux issus des points A et B de la tour et donne la position et la taille de l'image A"B" de celle-ci à travers le téléobjectif (l'échelle choisie étant arbitraire).
Afin de déterminer les caractéristiques de l'image ainsi formée, on utilise la méthode des images intermédiaires :
\(F'_1\) est l'image de A (situé à l'infini) par la lentille \((L_1)\) et \(A"\) est l'image de \(F'_1\) par la lentille \(L_2\).
La formule de conjugaison (avec origine au centre O2) pour la lentille (L2) donne :
\(- \frac{1}{{\overline {O_2 F'_1 } }} + \frac{1}{{\overline {O_2 A"} }} = \frac{1}{{f'_2 }}\)
Soit, avec \(f'_2=-25\;mm\) et \(\overline {O_2 F'_1}=18,8\;mm\), \(\overline {O_2 A"}=75,8\;mm\) : l'image de la base A de la tour est ainsi située à 7,58 cm du centre O2 de la lentille (L2).
L'encombrement du téléobjectif étudié est alors donné par :
\(\overline {O_1 A"} = \overline {O_1 O_2 } + \overline {O_2 A"} = 107\,mm = 10,7\,cm\)
A travers la 1ère lentille, l'image de la tour est l'image A'B' définie à la première question.
Cette image A'B' devient objet pour la 2nde lentille et la formule du grandissement écrite (avec origine au centre O2) pour cette dernière lentille donne alors :
\(\gamma = \frac{{\overline {A"B"} }}{{\overline {A'B'} }} = \frac{{\overline {O_2 A"} }}{{\overline {O_2 F'_1 } }}\)
D'où, avec (1ère question) \(\overline {A'B'} = -({AB} /D)\,f'_1\), la taille de l'image A"B" :
\(\overline {A"B"} = - \frac{{\overline {O_2 A"} }}{{\overline {O_2 F'_1 } }}\,\frac{{\overline {AB} }}{D}\,\,f'_1 = - 5\,mm\)
La taille de l'image obtenue est ainsi environ 4 fois plus grande que celle obtenue avec l'objectif standard de la 1ère question.