Cohérence temporelle et fentes d'Young ; déplacement et brouillage des franges
(15 minutes de préparation)
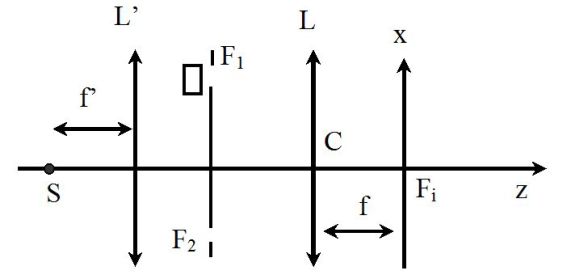
On considère le dispositif interférentiel des fentes d'Young, avec observation dans le plan focal d'une lentille mince convergente (L).
On donne :
\(F_1 F_2 = a = 1\;mm\;;\;\lambda _0 = 600\;nm\;;\;f = 50\;cm\)
Question
Décrire la figure d'interférences observée ainsi que la répartition d'intensité I(x).
Solution
Le résultat est classique (voir rappels de cours). L'interfrange notamment vaut :
\(i = \frac{{{\lambda _0}f}}{a}\)
L'intensité est donnée par la formule de Fresnel :
\(I(x) = 2{I_0}(1 + \cos (\frac{{2\pi }}{{{\lambda _0}}}\frac{{ax}}{f}))\)
Question
On intercale sur le trajet de l'un des faisceaux une lame à faces parallèles d'épaisseur e et d'indice n. Les faces sont perpendiculaires à l'axe de symétrie.
Déterminer le nombre N de franges qui ont défilées en Fi.
On prendra nair = 1, n = 1,5 et e = 0,5 mm.
Solution
La nouvelle différence de marche est :
\(\delta = \frac{{ax}}{f} - (n - 1)e\)
La position de la frange centrale devient (elle est obtenue pour une différence de marche nulle) :
\({x_0} = (n - 1)\frac{{ef}}{a}\)
L'interfrange n'a pas varié et le nombre de franges qui ont défilé est :
\(N = \frac{{{x_0}}}{i} = (n - 1)\frac{e}{{{\lambda _0}}} = 416\)
Question
On supprime la lame à faces parallèles.
Les fentes sont maintenant éclairées par le doublet jaune du sodium formé de deux radiations, supposées monochromatiques et de même intensité, de longueurs d'onde :
\(\lambda _1 = 589,0\;nm\) et \(\lambda _2 = 589,6\;nm\)
A quelle distance de la frange centrale les franges disparaissent-elles pour la 1ère fois ?
Solution
Qualitativement, le premier brouillage apparaît lorsqu'une frange sombre correspondant à λ1 se superpose à une frange brillante associée à λ2, soit pour un ordre d'interférence p vérifiant :
\(x = (p + \frac{1}{2}){i_1} = p{i_2}\)
Où :
\(i_1 = \frac{{{\lambda _1}f}}{a}\) et \(i_2 = \frac{{{\lambda _2}f}}{a}\)
On en déduit :
\(p = \frac{{{i_1}}}{{2({i_2} - {i_1})}} = \frac{{{\lambda _1}}}{{2({\lambda _2} - {\lambda _1})}}\)
Puis la valeur de l'abscisse où se produit le brouillage :
\(x = \frac{{{\lambda _1}}}{{2({\lambda _2} - {\lambda _1})}}{i_2} = \frac{{{\lambda _1}{\lambda _2}}}{{2({\lambda _2} - {\lambda _1})}}\frac{f}{a} = \frac{{\lambda _0^2}}{{2\Delta \lambda }}\frac{f}{a} = 14,5\;cm\)
Où on a posé :
\({\lambda _0} = \frac{{{\lambda _1} + {\lambda _2}}}{2}\)
La valeur moyenne des deux longueurs d'ondes.