Thermal convection
Fondamental : Convective heat transfer (convection)
Conducto-convective transfer :
It is commonly noticed that, in order to cool down some hot liquid in a bottle, we shake this bottle.
So do the parents before giving the bottle to their baby.
The thermal transfer through the walls of the bottle is done by diffusive thermal conduction.
The agitation of the liquid results inconvective movements that foster thermal conduction through the walls.
Another example is the conducto-convective exchange between the air in a room and the surface of the radiator used to heat this room.
In order to model those examples, let's consider a unidirectional model in stationnary mode, as represented on the following picture:
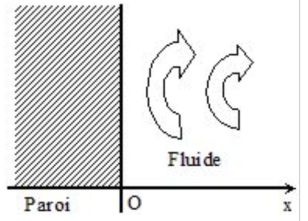
The convection movements into the fluid lead to a homogenization of the temperature.
Let's consider that the stirring is sufficient to make the temperature spatially constant, equaling \(T_f\).
However, in the walls, the transfer is conductive, along the \((Ox)\) axis.
We can observe a temperature gradient.
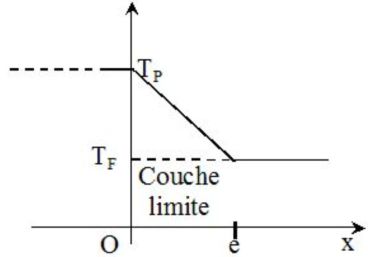
The temperature of the wall is not the same as the temperature of the fluid : a boundary layer with a small thickness noted \(e\) (some \(mm\)) exists.
The fluid is nearly motionless in it and the heat transfer is a conductive one.
Attention : Newton's Law
The algebraic thermal transfers bewteen a body and the external medium follow Newton's law if the thermal flux density that through the surface of the material is proportionnal to the temperature difference between the one of the surface and the one of the external medium.
With the notations of the previous paragraph :
\({j_{conv}}=h({T_P}-{T_F})\)
\(h\) is the coefficient of convective heat transfer.