Experimental measurement of a thermal conductivity
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
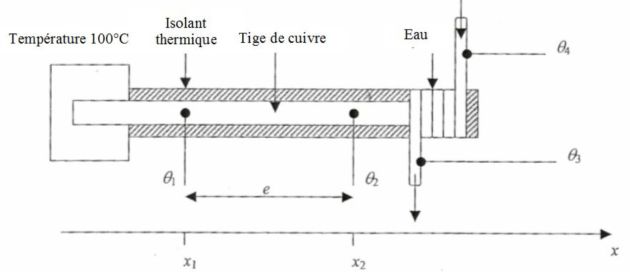
We put the following montage into place in order to measure the thermal conductivity of copper, \(K\).
The left edge of the cylindrical copper bar, of \(S = 11,5\;cm^2\), is placed in an oven at the temperature \(100°C\).
We note \(\mu\) the density of the copper and \(c_{Cu}\) its mass thermal capacity.
The other edge is in contact with a coil in which water circulates (with \(c = 4,18 \;kJ.K^{-1}.kg^{-1}\) its mass thermal capacity) with a mass flow \(D_m = 0,80\; g.s^{-1}\).
The heat exchanger so made allows water to be overheated from \(\theta_4\) to \(\theta_3\).
The bar is laterally insulated, with insulating covers.
We measure the temperatures \(\theta_1\) and \(\theta_2\) of the bar, at two different points of it, with \(e=10\;cm\) between them, and also the temperatures \(\theta_4\) and \(\theta_3\) of water just before and after the heat exchange zone.
The problem is one-dimensional, the material is homogeneous and any convection or radiation phenomenon on the bar will be neglected.
Question
Why is the bar laterally insulated ? Give an example of insulating material that could be used for this experiment.
Solution
Insulating material : glass wool or polystyrene foam.
Question
We wait for the stationary mode to be put into place. After applying the heat conduction equation, express the temperature \(T(x)\) along the bar using \(x\), the constants \(x_1\), \(e\), \(T_1\) and \(T_2\).
Solution
The heat conduction equation is :
\(\frac{{\partial T}}{{\partial t}} = \frac{K}{{\mu {c_{Cu}}}}\frac{{{\partial ^2}T}}{{\partial {x^2}}}\)
In stationary mode :
\(T(x) = {T_1} + \frac{{{T_2} - {T_1}}}{e}(x - {x_1})\)
Question
Determine the thermal power through the \(S\) section in the bar. Does it depend on \(x\) ?
Solution
The thermal power is a constante :
\(\Phi = -SK\frac{dT(x)}{dx}=- KS\frac{{{T_2} - {T_1}}}{e}\)
Question
Determine the thermal power received by the water in the coil using \(\theta_4\) and \(\theta_3\) (you can first make a balance on the water mass \(dm\) circulating in the coil during \(dt\))
Solution
The first law of thermodynamics gives :
\(dU \approx dH = dm\;c\;({\theta _3} - {\theta _4}) = \delta Q + \delta W = {P_{th}}dt\)
Thus :
\({P_{th}} = {D_m}c({\theta _3} - {\theta _4})\)
Question
Deduce the expression of the thermal conductivity of copper \(K\).
Experimentally, we obtain \(K= 374\). Give its units.
Solution
The exchanger is ideal :
\({P_{th}} = {D_m}c({\theta _3} - {\theta _4}) = \Phi = - KS\frac{{{T_2} - {T_1}}}{e}\)
Thus :
\(K = \frac{{{D_m}ce}}{S}\frac{{{\theta _3} - {\theta _4}}}{{{\theta _1} - {\theta _2}}} = 374\;W.{m^{ - 1}}.{K^{ - 1}}\)