Scattering of peak concentrations
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
A pipe of \(L\) length, \(S\) section, is long enough by the \((Ox)\) axis and the times are short enough to neglect the edge effect.
At the initial time, the molecules we are studying are very concentrated into the \((Oxy)\) plan, and \(N_0\) is their number.
They scatter in a supporting fluid and \(D\) is their scattering coefficient.
Question
What is the condition on \(a\) for the function :
\(n(x,t) = \frac{K}{{\sqrt t }}{e^{ - \frac{{a{x^2}}}{t}}}\)
to be solution of the diffusion equation ?
Solution
The diffusion equation of the molecules is :
\(D\frac{{{\partial ^2}n}}{{\partial {x^2}}} = \frac{{\partial n}}{{\partial t}}\)
With :
\(n(x,t) = \frac{K}{{\sqrt t }}{e^{ - \frac{{a{x^2}}}{t}}}\)
We calculate :
\(\frac{{{\partial ^2}n}}{{\partial {x^2}}} = - \frac{{2aK}}{{{t^{3/2}}}}\left( {1 - \frac{{2a{x^2}}}{t}} \right){e^{ - \frac{{a{x^2}}}{t}}}\)
\(\frac{{\partial n}}{{\partial t}} = - \frac{K}{{2{t^{3/2}}}}\left( {1 - \frac{{2a{x^2}}}{t}} \right){e^{ - \frac{{a{x^2}}}{t}}}\)
The equation is solved if :
\(a = \frac{1}{{4D}}\)
Question
What is the value of \(K\) for it to satisfy the initial conditions ?
Draw the appearane of the graph of \(n(x,t)\) at \(t_1\) and \(t_2 > t_1\).
Solution
This solution is such that it verifies :
The initial condition \(n(x \ne 0,t = 0) = 0\) because at \(t=0\), all the molecules are at \(x=0\).
The edge condition \(n(x = \pm \infty ,t) = 0\), because the scattering does not reach the edges of the pipe.
The conservation of the number of molecules in the pipe still remains to be interpreted :
\({N_0} = \int_{ - \infty }^{ + \infty } {n(x,t)Sdx} = \frac{{KS}}{{\sqrt t }}\int_{ - \infty }^{ + \infty } {{e^{ - \frac{{{x^2}}}{{4Dt}}}}dx}\)
The variable substitution :
\(u = \frac{x}{{2\sqrt {Dt} }}\)
Gives :
\({N_0} = 2KS\sqrt D \int_{ - \infty }^{ + \infty } {{e^{ - {u^2}}}du} = 2KS\sqrt {\pi D}\)
So :
\(K = \frac{{{N_0}}}{{2S\sqrt {\pi D} }}\)
And finally :
\(n(x,t) = \frac{{{N_0}}}{{2S\sqrt {\pi D} }}{e^{ - \frac{{{x^2}}}{{4Dt}}}}\)
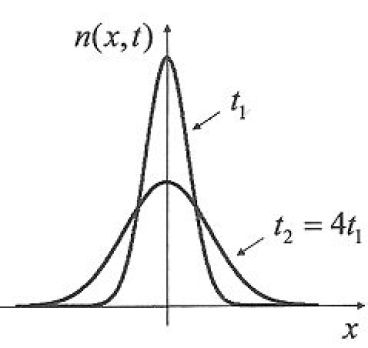
Over time, this Gaussian profile widens and flattens, the area under the graph, linked to the number of molecules, remains constant.
Question
Give the probability \(dP = p(x,t)dx\) for a molecule to be at the moment \(t\) in the \(x\) layer (of \(dx\) thickness) and deduce the average abscissa \(<x>\) and the average quadratic distance \(x_m\).
We give :
\(\int_{ - \infty }^{ + \infty } {{e^{ - {u^2}}}} du = \sqrt \pi\) and \(\int_{ - \infty }^{ + \infty } {{u^2}{e^{ - {u^2}}}} du = \frac{{\sqrt \pi }}{2}\)
Solution
If \(dN=n(x,t)Sdx\) is the number of molecules at \(t\) in the layer of \(dx\) thickness, the probability is :
\(dP = \frac{{dN}}{{{N_0}}} = \frac{1}{{2\sqrt {\pi Dt} }}{e^{ - \frac{{{x^2}}}{{4Dt}}}}dx\)
So :
\(< x > = \int_{ - \infty }^{ + \infty } {xp(x,t)dx} = 0\)
by integrating an odd function on a symetrical interval.
The average position of the molecules (their barycenter) is at \(x=0\) because the scattering is symetrical around this plan.
The average quadratic distance \(x_m\) is such that :
\(x_m^2 = < {x^2} > = \int_{ - \infty }^{ + \infty } {{x^2}p(x,t)dx}\)
That is to say :
\(x_m^2 = \int_{ - \infty }^{ + \infty } {\frac{{{x^2}}}{{2\sqrt {\pi Dt} }}{e^{ - \frac{{{x^2}}}{{4Dt}}}}dx} = \sqrt {2Dt}\)
The average quadratic distance grows like the square root of time, it means that over time, this distance spreads slower and slower.
The diffusion is said to downturn, which is characteristic.
Question
If we have for solute in water \( D=2.10^{-9 }\;m^2.s^{-1}\), estimate the time needed for the scattering to reach \(1\; mm\) and \(1\;cm\).
Solution
For \(x_m=1\;mm\), \(t\) is about\(4\) minutes, while \(7\) hours are needed to reach \(1\;cm\).