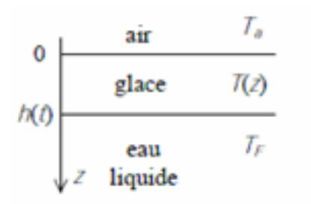
A lake freezes
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
The temperature of the air is \(T_a=263\;K\) and the temperature of the liquid water is \(T_F=273\;K\).
We give the massic latent heat of fusion of ice \(L_f\), its density \(\rho\) and its thermal conductivity \(\lambda\).
The thermal capacity of ice is supposed to be negligible.
Let \(h(t)\) be the height of ice at time \(t\). At \(t=0\), \(h(0)=0\).
Question
Establish the differential equations which have \(T(z)\) and \(h(t)\) as solutions.
Solve them and determine \(h(t)\).
Solution
The heat equation in the ice :
\(\rho c\frac{{\partial T}}{{\partial t}} = \lambda \frac{{{\partial ^2}T}}{{\partial {z^2}}}\)
So if we suppose that \(c\) is almost \(0\) :
\(\frac{{{\partial ^2}T}}{{\partial {z^2}}} \approx 0\)
So :
\(T(z,t) = {T_a} + \frac{{{T_F}-{T_a}}}{{h(t)}}z\)
We make the approximation of the quasi-stationary mode.
The heat flow in the ice is due to its solidification, that is to say, between \(t\) and \(t+dt\) :
\(j(z,t) = - \lambda \frac{{\partial T}}{{\partial z}} = - \frac{{\lambda ({T_F}-{T_a})}}{{h(t)}}\)
So :
\(- \frac{{\lambda ({T_F}-{T_a})}}{{h(t)}}Sdt = - {L_F}dm = - \rho Sdh{L_F}\)
That is to say :
\(\frac{{\lambda ({T_F}-{T_a})}}{{h(t)}}Sdt = \rho Sdh{L_F}\)
And :
\(hdh = \frac{{\lambda ({T_F}-{T_a})}}{{\rho {L_F}}}dt\)
After integration :
\(h = \sqrt {\frac{{2\lambda ({T_F}-{T_a})}}{{\rho {L_F}}}\;t}\)