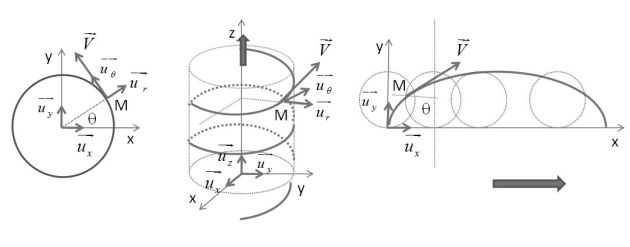
Kinematics in a frame of reference
Fondamental : Velocity vector
In polar coordinates :
\(\vec v = \dot r\;{\vec u_r}+r\dot \theta \;{\vec u_\theta }\)
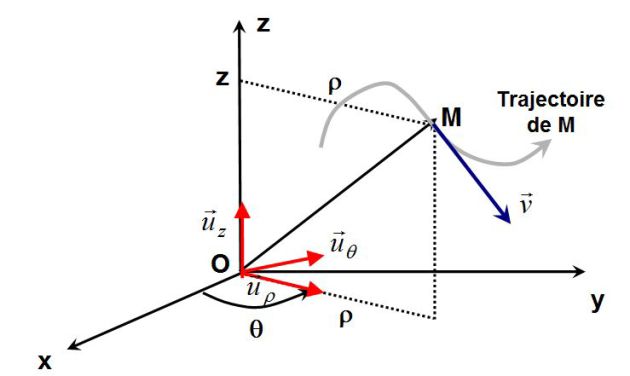
In cylindrical coordinates :
\(\vec v = \dot \rho {\vec u_\rho } + \rho \dot \theta {\vec u_\theta } +\dot z{\vec u_z}\)
In spherical coordinates :
\(\vec v = \dot r{\vec u_r} + r\dot \theta {\vec u_\theta } + r\sin \theta \dot \varphi {\vec u_\varphi }\)
Fondamental : Acceleration vector
In polar coordinates :
\(\vec a = (\ddot r - r{\dot \theta ^2})\;{\vec u_r} + (r\ddot \theta + 2\dot r\dot \theta )\;{\vec u_\theta }\)
In cylindrical coordinates :
\(\vec a = (\ddot \rho - \rho {\dot \theta ^2})\;{\vec u_\rho } + (\rho \ddot \theta + 2\dot \rho \dot \theta )\;{\vec u_\theta } + \;\ddot z\;{\vec u_z}\)
Exemple : Circular motion
Let \(r=OM=R\) be the radius of a circle.
The angular velocity vector is :
\(\vec \omega = \omega \;\vec u_z = \dot \theta \;\vec u_z\)
Where \(\theta\) is the usual angle of polar coordinates.
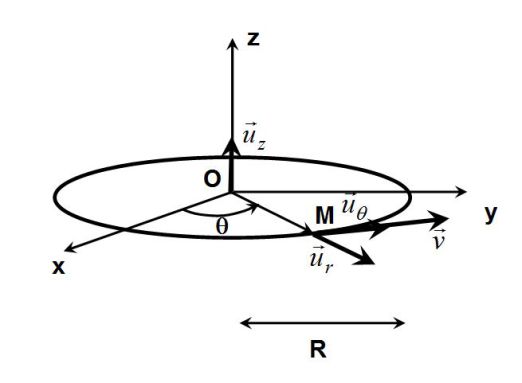
The velocity vector is :
\(\vec v=R \dot \theta \vec u_{\theta}\)
The acceleration vector is :
\(\vec a\; = \; - R{\dot \theta ^2}\;{\vec u_r}\; + \;R\ddot \theta \;{\vec u_\theta }\; = \; - \frac{{{v^2}}}{R}\;{\vec u_r}\; + \;R\dot \omega \;{\vec u_\theta }\)
If we consider a uniform motion (\(\omega = cste\)) :
\(\vec a\; = \; - \frac{{{v^2}}}{R}\;{\vec u_r}\;\)
The acceleration is purely centripetal.
A few exemples of motions of a material point :