Kinematics : changing the frame of reference
Remarque : Relativity on motion
Trajectories change when the reference frame does.
The movement of a point is not the same when it is studied in another frame of reference : it is relative to the frame.
Problem :
We know the movement of a material point in a reference frame (R).
How is a point moving when it is studied in a reference frame (R') which is moving relative to (R) ?
For instance :
What trajectory does the moon describe relatively to the sun ?
Simulation : A JAVA animation by Jean-Jacques Rousseau (Université du Mans)
Motion of the Moon : click
Fondamental : Pure translation of reference frames
A rigid body is in translation if all of its points have at all times the same velocity vector.
For exemple, a Ferris wheel is in circular translation relative to its axis, and the Earth is in circular translation relative to the sun.
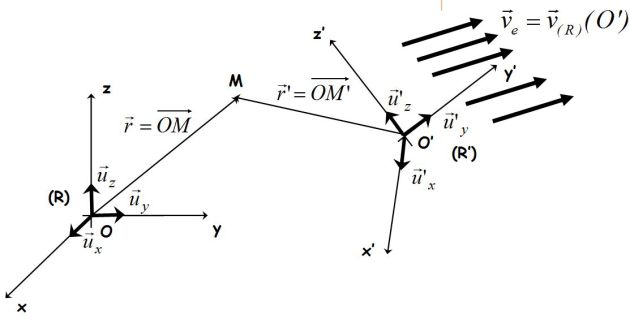
The next figure explicits the chosen notations.
The \((R')\) reference frame, which we describe by the Cartesian coordinates \((O'x'y'z')\) is moving in translation relatively to the \((R)\) frame, at the speed of the \((O')\) point in this frame.
We can also note that the basis vectors of \((R')\) (\(\vec u'_x, \vec u'_y,\vec u'_z\)) keep fixed directions.
Composition of velocity :
We can decompose the vector :
\(\vec r = \overrightarrow {OM} = \overrightarrow {OO'} + \overrightarrow {O'M}\)
Let us calculate the velocity in \((R)\) :
\({(\vec v)_R} = \vec v = {\left( {\frac{{d\overrightarrow {OM} }}{{dt}}} \right)_R} = {\left( {\frac{{d\overrightarrow {OO'} }}{{dt}}} \right)_R} + {\left( {\frac{{d\overrightarrow {O'M} }}{{dt}}} \right)_R}\)
The index \((R)\) means that velocity \(\vec v\) is calculated in the \((R)\) referential frame, in which the basis vectors \((\vec u_x, \vec u_y,\vec u_z)\) are constant.
Most of the time, the basis vectors of \((R')\) \((\vec u'_x, \vec u'_y,\vec u'_z)\) evolve through time.
When the movement is a translation, these vectors are constant, thus we can simplify the relation :
\(\;{\left( {\frac{{d\overrightarrow {O'M} }}{{dt}}} \right)_R} = \;\frac{d}{{dt}}{\left( {x'\vec u \;{'_x} + y'\vec u \;{'_y} + z'\vec u \;{'_z}} \right)_R} = \dot x'\vec u \;{'_x} + \dot y'\vec u \;{'_y} + \dot z'\vec u \;{'_z} = \vec v \;'\)
Finally : (composition of velocity)
\(\vec v(M) = \;\vec v \;'(M) + \vec v(O')\)
Composition of acceleration :
In the same way :
\(\vec a(M) = \;\vec a \;'(M) + \vec a(O')\)
We can see that for a uniform translation :
\(\vec a(M) = \;\vec a \;'(M)\)
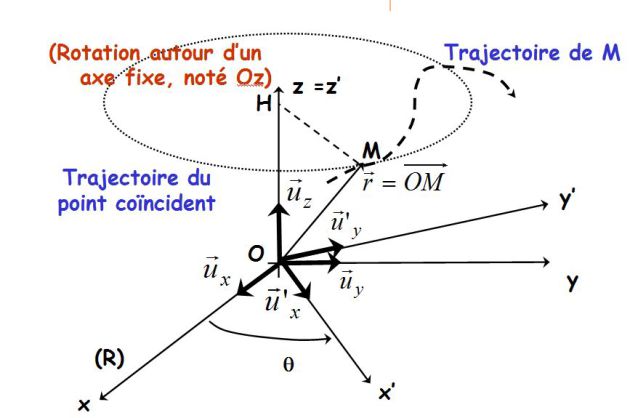
Fondamental : Pure rotation of reference frames
The frame of reference \((R')\) is in rotation around the axis \((Oz)\) of the "fixed" frame \((R)\) (see figure) :
We write :
\(\begin{array}{l}\vec r = \overrightarrow {OM} = x{{\vec u}_x} + y{{\vec u}_y} + z{{\vec u}_z} \\\;\;\;\;\;\;\;\;\;\;\; = x'\vec u \;{'_x} + y'\vec u \;{'_y} + z{\vec u _z} \\\end{array}\)
We write :
\(\theta = ({\vec u_x},\vec u \;{'_x})\;\;\;;\;\;\;\omega = \dot \theta \;\;\;and\;\;\;\vec \omega = \omega \;{\vec u_z}\)
\(\vec \omega\) is the angular velocity vector of the \((R')\) frame relative to \((R)\).
We will use : (see the kinematics courses on the derivatives of polar vectors)
\({\left( {\frac{{d\vec u \;{'_x}}}{{dt}}} \right)_R} = \dot \theta \;\vec u \;{'_y} = \;\omega \;\vec u \;{'_y}\;\;\;\;\;;\;\;\;\;\;{\left( {\frac{{d\vec u \;{'_y}}}{{dt}}} \right)_R} = - \dot \theta \;\vec u \;{'_x} = - \omega \;\vec u \;{'_x}\)
Composition of velocity :
Let us express the velocity vector :
\(\vec v = {\left( {\frac{{d\overrightarrow {OM} }}{{dt}}} \right)_R} = \frac{d}{{dt}}{\left( {x'\vec u \;{'_x} + y'\vec u \;{'_y} + z{{\vec u}_z}} \right)_R} = \vec v \;' + x'\frac{{d\vec u \;{'_x}}}{{dt}} + y' \frac{{d\vec u \;{'_y}}}{{dt}}\)
We find :
\(\vec v = {\left( {\frac{{d\overrightarrow {OM} }}{{dt}}} \right)_R} = \vec v \;' + (x'\dot \theta \;\vec u \;{'_y} - y'\dot \theta \;\vec u \;{'_x})\)
We know :
\(\vec \omega \wedge \overrightarrow {OM} = \dot \theta \;{\vec u_z} \wedge (x'\vec u \;{'_x} + y'\vec u \;{'_y} + z{\vec u_z}) = (x'\dot \theta \; \vec u \;{'_y} - y'\dot \theta \;\vec u \;{'_x})\)
From where we can derive the composition of velocity :
\(\vec v = \vec v \;' + \vec \omega \wedge \overrightarrow {OM} = \vec v \;' + {\vec v_e}\;\;\;\;\;with\;\;\;\;\;{\vec v_e} = \vec \omega \wedge \overrightarrow {OM}\)
Sidenote : temporal derivative and change of reference frame
\(\vec v = \vec v \;' + \vec \omega \wedge \overrightarrow {OM} \;\;\;\;\;so\;\;\;\;\;{\left( {\frac{{d\overrightarrow {OM} }}{{dt}}} \right)_R} = \;{\left( {\frac{{d\overrightarrow {OM} }}{{dt}}} \right)_{R'}} + \vec \omega \wedge \overrightarrow {OM}\)
We can generalize this formula for any \(\vec A\) vector :
\({\left( {\frac{{d\vec A}}{{dt}}} \right)_R} = {\left( {\frac{{d\vec A}}{{dt}}} \right)_{R'}} + \vec \omega \wedge \vec A\)
This is the relation we will use to determine the composition of acceleration vectors.
Composition of acceleration :
Let us use the former relation :
\(\vec a = {\left( {\frac{{d\vec v}}{{dt}}} \right)_R} = {\left( {\frac{{d\vec v}}{{dt}}} \right)_{R'}} + \vec \omega \wedge \vec v\)
Then :
\(\vec a = \frac{d}{{dt}}{\left( {\vec v \;' + \vec \omega \wedge \overrightarrow {OM} } \right)_{R'}} + \vec \omega \wedge \left( {\vec v \;' + \vec \omega \wedge \overrightarrow {OM} } \right)\)
\(\vec a = {\left( {\frac{{d\vec v \;'}}{{dt}}} \right)_{R'}} + {\left( {\frac{{d\vec \omega }}{{dt}}} \right)_{R'}} \wedge \overrightarrow {OM} + \vec \omega \wedge {\left( {\frac{{d\overrightarrow {OM} }}{{dt}}} \right)_{R'}} + \vec \omega \wedge \vec v \;' + \vec \omega \wedge \left( {\vec \omega \wedge \overrightarrow {OM} } \right)\)
From which we extract :
\(\vec a = \vec a \;' + \left( {\frac{{d\vec \omega }}{{dt}} \wedge \overrightarrow {OM} + \vec \omega \wedge \left( {\vec \omega \wedge \overrightarrow {OM} } \right)} \right) + 2\vec \omega \wedge \vec v \;'\)
And finally : (Composition of acceleration)
The Coriolis acceleration is equal to zero if the point \(M\) is at rest in \((R')\).
For a uniform rotation (ω= cste) :
We can evaluate the term :
\({\vec a_e} = \;\vec \omega \wedge \left( {\vec \omega \wedge \overrightarrow {OM} } \right)\)
A useful mathematic reminder :
\(\vec a \wedge \left( {\vec b \wedge \vec c} \right) = (\vec a.\vec c)\;\vec b - (\vec a.\vec b)\;\vec c\)
If we apply this :
\({\vec a_e} = (\;\vec \omega .\overrightarrow {OM} )\;\vec \omega - (\vec \omega .\vec \omega )\;\overrightarrow {OM} = (\;\vec \omega .\overrightarrow {OM} )\;\vec \omega - {\omega ^2}\;\overrightarrow {OM}\)
Let H be the orthogonal projection of M on the axis \((Oz)\) :
\(\vec \omega .\overrightarrow {OM} = \omega \;OH\)
We can see :
\({\vec a_e} = (\omega .OH)\;\vec \omega - {\omega ^2}\;\overrightarrow {OM} = {\omega ^2}(\overrightarrow {OH} - \overrightarrow {OM} ) = {\omega ^2}(\overrightarrow {OH} + \overrightarrow {MO} ) = {\omega ^2}\overrightarrow {MH}\)
Finally :
\({\vec a_e} = - {\omega ^2}\overrightarrow {HM}\)
We find the acceleration of a uniform circular motion.