Work pressure forces : energy exchange of macroscopic origin, that is to say, the work of forces defined our scale and acting on the surface defining the system.

Consider a cylinder closed by a movable piston.

The external pressure force is :

\({\vec f_{ext}} = - \;{P_{ext}}S\;{\vec u_x}\)

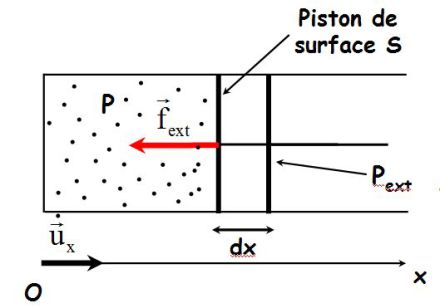
At an elementary movement of the piston, the work is :

\(\delta {W_{ext}} = {\vec f_{ext}}.(dx\;{\vec u_x}) = ( - \;{P_{ext}}S\;{\vec u_x}).(dx\;{\vec u_x})\)

Is :

\(\delta {W_{ext}} = - \;{P_{ext}}S\;dx\)

But, \(Sdx=dV\) (variation in the volume of gas, which is \(> 0\) in the drawing), as follows :

\(\delta {W_{ext}} = - \;{P_{ext}}\;dV\)

So :

• If \(dV<0\) (volume decreases) : work is positive (the gas receives energy in the form of work).

• If \(dV>0\) (volume increases) : the work is negative (the gas expands and provides work to the outside).

This result can be generalized to any volume (gas, liquid, solid).

Thus, the work received from the external pressure forces by a thermodynamic system which has a volume varying \(dV\) is :

\(\delta {W_{ext}} = - \;{P_{ext}}\;dV\)

At a reversible transformation, the external pressure is constantly equal to the internal pressure \(P\), that is to say that of the system.

Therefore, the work of the pressure forces is :

\(\delta {W_{ext}} = - \;P\;dV\;\;\;\;\;and\;\;\;\;\;{W_{ext}} = - \;\int_{{V_1}}^{{V_2}} {P\;dV}\)

If the volume remains constant, the work of the pressure forces is zero.

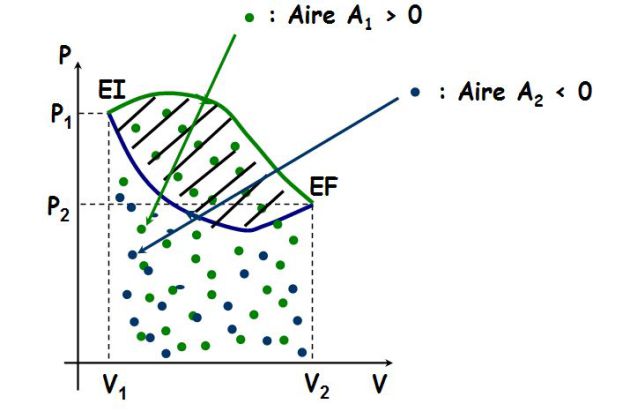
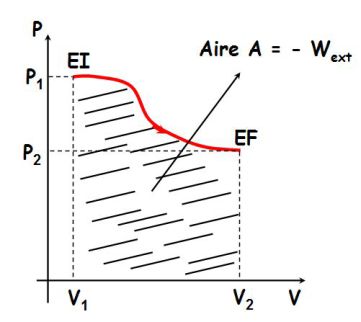
Geometric interpretation of the work :

\({W_{ext}} = - \;\int_{{V_1}}^{{V_2}} {P\;dV} = - A\)

Where \(A\) is the curve area (see figure).

Here, \(A>0\) and \(W_{ext}<0\) :

The gas receives a negative work (it provides energy in the form of work to the outside since it expands).

The \((P, V)\) plane is called Clapeyron plane (coordinates of Clapeyron) ; attention \(P\) is ordinate and \(V\) abscissa !

The work depends on the path taken to get the same initial state to the same final state, as shown in the following figure :

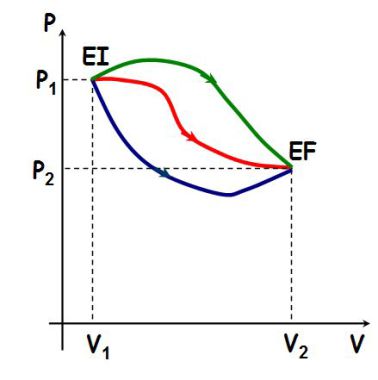
Areas defined by each of the three curves are different each time ; therefore, the work received by a system depends on the path followed and not only depends on the initial state and the final state.

The work is not a state function.

Do not write : \(dW\) (but write \(\delta W\)).

Do not write : \(\Delta W=W_f-W_i\) (but but write \(W\)).

A reversible cycle :

The total area enclosed by the cycle gives the opposite of the total work received by the system which performs the cycle.

Here, \(W < 0\) : the cycle is motor.

• Transformation at constant volume : \(W=0\)

• Transformation at constant external pressure \(P_{atm}\) for instance :

• \(\delta {W_{ext}} = - {P_{ext}}dV = - {P_{atm}}dV\;\;\;\;;\;\;\;\;{W_{ext}} = - {P_{atm}}({V_2} - {V_1})\)

• Isothermal reversible transformation of a perfect gas :

  Diathermic walls : walls that allow the heat pass through (unlike adiabatic walls or athermanous).

  Thermostat (or heat source) : a very large body, whose temperature remains constant (here equal to \(T_0\)) even when the body receives heat.

  Here, the ideal gas undergoes a reversible transformation at constant temperature ; we speak of isothermal transformation.

  Using the equation of state of perfect gas :

  \(\delta W = - \frac{{nR{T_0}}}{V}dV = - nR{T_0}\frac{{dV}}{V}\)

  And the total work received by the gas during the transformation is :

  \(W = - nR{T_0}\int_{{V_1}}^{{V_2}} {\frac{{dV}}{V}} = - nR{T_0}\ln \left( {\frac{{{V_2}}}{{{V_1}}}} \right)\)

  Knowing that (Mariotte's law) :

  \({P_1}{V_1} = {P_2}{V_2} = nR{T_0}\)

  It becomes :

  \(W = - nR{T_0}\ln \left( {\frac{{{V_2}}}{{{V_1}}}} \right) = - nR{T_0}\ln \left( {\frac{{{P_1}}}{{{P_2}}}} \right)\)

  And :

  \(W = - {P_1}{V_1}\ln \left( {\frac{{{V_2}}}{{{V_1}}}} \right) = - {P_1}{V_1}\ln \left( {\frac{{{P_1}}}{{{P_2}}}} \right)\)

Thermal transfer ("Heat") energy exchange at the microscopic level (eg rigid container containing a gas and placed on a hot plate).

Heat transfer is noted \(Q\) received by a system (algebraic quantity \(>\) or \(<0\)).

Historically, the \(calorie\) is used : \(1\; cal = 4,18\; J \) :

"The calorie is the amount of heat required to raise the temperature of one gram of water by \(1 ° C\) (\(1 K\)) at constant pressure of \(1 \;bar\) and from \(14.5 ° C\)".

Some orders of magnitude :

• \(1 \;kg\) of water is heated from \(20 ° C\) to \(100 ° C\) under \(1 \;bar\) :

  \(Q = 80 \;kcal = 334,4 \;kJ\)

• Converting \(1\; kg\) of liquid water to steam at \(100 ° C\) under \(1 \;bar\) :

  \(Q = 2 \;255\; kJ\)

  \(Q\) is here called the latent heat of vaporization of water.