Ampère's circuital law
Presentation of electricity and magnetism video (Référence : "Physique collégiale")
Fondamental :
Stokes theorem, which we use without demonstration, is the equivalent of Ostrogradsky's theorem.
Stokes' theorem :
Let \((C)\) be an oriented closed loop and \((S)\) a given surface which is supported by \((C)\) (as if it was a hat and \((C)\) was the extremity).
The normal vector of the surface \((S)\) is oriented with the Right-hand rule.
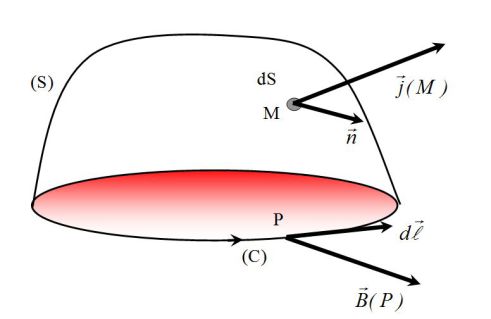
\(\oint_{(C)} {\vec B..d\vec r} = \iint_S \overrightarrow {rot} \;\vec B.\vec n\;dS\)
This theorem allows us to write Ampère's circuital law in its integral form.
Maxwell- Ampère equation in static regime is :
\(\;\overrightarrow {rot} \;\vec B = \mu _0 \vec j\)
We compute the line integral of the magnetic field around a closed loop \((C)\) at a given moment. A surface \((S)\) is supported by \((C)\).
Let's use the Maxwell- Ampère equation :
\(\oint_{(C)} {} \vec B.d\vec \ell =\iint_S \overrightarrow {rot} \;\vec B.\vec n\;dS =\iint_S{\mu _0}\vec j.\vec n\;dS\)
We recognize :
\(i = \iint \vec j.\vec n\;dS\)
The intensity going through \((S)\).
Hence Ampère's circuital law is :
\(\oint_{(C)} {} \vec B.d\vec \ell =\iint_S{\mu _0}\vec j.\vec n\;dS=\mu_0 i\)
Attention : Flux and circulation of B (Ampère's circuital law)
The flux piercing through a closed surface of \(\vec B\) is equal to zero :
\( \oint_S\vec {B}.\vec{n} \ dS=0\)
Ampère's circuital law :
\(\oint_{(C)} {} \vec B.d\vec \ell =\iint_S{\mu _0}\vec j.\vec n\;dS=\mu_0 i\)
Méthode : Classic use of Ampere's circuital law
Ampère's circuital law helps computing easily a magnetic field in a highly symmetrical problem, especially in these must-know classic examples :
Infinite wire (without thickness) crossed by a current \(I\) :
\(\vec B=\frac{\mu_0 I}{2\pi}\frac{1}{r}\vec u_{\theta}\)
The cylindrical base is used.
Infinitely long solenoid, composed of \(n\) whorls by length unit, crossed by a current \(I\) :
\(\vec B_{ext}=\vec 0\)
\(\vec B_{int}=\mu_0 n I \;\vec u_z\)

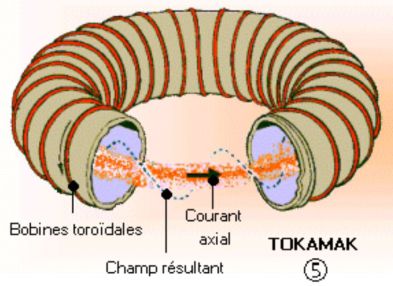
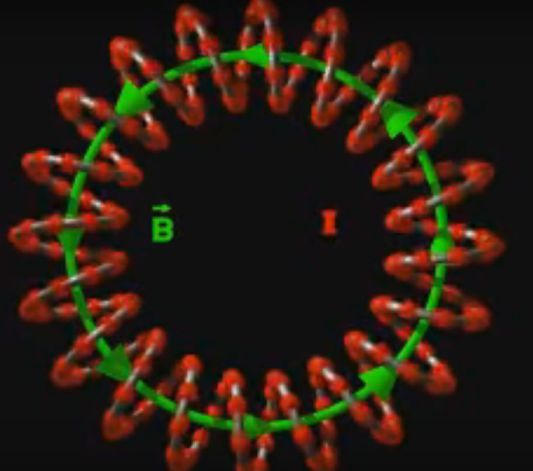
Magnetic field created by a torus (the one from the picture above), composed of \(N\) whorls crossed by current \(I\) :
\(\vec B_{ext}=\vec 0\)
\(\vec B_{int}=\frac {\mu_0 N I}{2\pi r} \vec u_{\theta}\)
The cylindar base is used.