Clamp ammeter
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
The usual ammeters cannot bear high intensities (in general \(I_{max}=10A\))
To measure higher intensities, a clamp ammeter is used.
The principle is studied here.
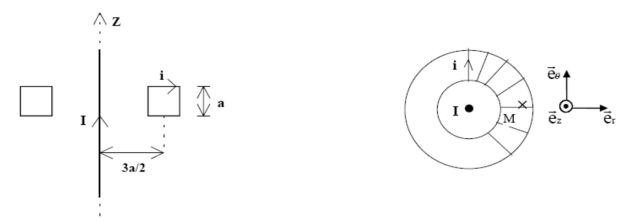
An infinite straight wire of axis \((Oz)\) is travelled by a current (the one we want to measure) of intensity :
\(I(t)=I_{max} cos(\omega t)\)
The wire is surrounded by a winding made of a square-section torus of side a and medium radius \(3a / 2\).
On the torus are regularly wound a great number \(N\) of whorls.
This winding is closed on an ammeter.
The circuit created has a total resistance \(R\) and is travelled, by induction, by a sinusoidal current :
\(i(t)=i_{max} cos(\omega t+\phi)\)
Question
Compute the electromotive force induced by the current \(I(t)\).
Indice
There are two magnetic fields, hence two fluxes to compute.
Solution
The magnetic field due to the infinite wire is (apply Ampere's law), at a point inside the torus :
\(\vec B_{fil} = \frac{{\mu _0 I(t)}}{{2\pi }}\frac{1}{r}\vec u_\theta\)
The own magnetic field of the torus is (apply Ampere's law) :
\(\vec B_{tore} = \frac{{\mu _0 Ni(t)}}{{2\pi }}\frac{1}{r}\vec u_\theta\)
The total magnetic field is :
\(\vec B = \frac{{\mu _0 }}{{2\pi }}\left( {Ni(t) + I(t)} \right)\frac{1}{r}\vec u_\theta\)
The flux of this total field through the \(N\) whorls of the torus is :
\(\Phi = N = \frac{{N\mu _0 }}{{2\pi }}\left( {Ni(t) + I(t)} \right)a\ln 2\)
Hence the electromotive force can be deduced by using Faraday's law of induction :
\(e = - \frac{{d\phi }}{{dt}} = - \frac{{N\mu _0 }}{{2\pi }}\left( {N\frac{{di(t)}}{{dt}} + \frac{{dI(t)}}{{dt}}} \right)a\ln 2\)
Question
Compute the ratio :
\(\frac{{i_{\max } }}{{I_{\max } }}\)
\(R\) can be neglected before \(\mu _0 \omega aN^2\) .
Indice
Use complex notation.
Solution
The electric equation of the circuit is :
\(e = - \frac{{N\mu _0 }}{{2\pi }}\left( {N\frac{{di(t)}}{{dt}} + \frac{{dI(t)}}{{dt}}} \right)a\ln 2 = Ri\)
Which is, in complex notation :
\(- \frac{{N\mu _0 }}{{2\pi }}\left( {N\underline i (t) + \underline I (t)} \right)j\omega a\ln 2 = R\underline i\)
Thus :
\(\frac{{\underline i (t)}}{{\underline I (t)}} = \frac{{ - j\omega \frac{{\mu _0 }}{{2\pi }}Na\ln 2}}{{R + j\omega \frac{{\mu _0 }}{{2\pi }}N^2 a\ln 2}}\)
\(R\) can be neglected before \(\mu _0 \omega aN^2\) :
\(\frac{{\underline i (t)}}{{\underline I (t)}} = \frac{1}{N}\)
With a magnitude for \(N\) of \(10^4\), intensities can be measured with ammeters of small caliber.