Écoulement de Poiseuille
Remarque :
La méthode proposée dans cette fiche de cours, basée sur la résolution de l'équation de Navier - Stokes, est une méthode différente de celle présentée dans la vidéo "La physique animée".
Fondamental : Champs des vitesses et des pressions
En 1835 un médecin français, Poiseuille fit une série d'expériences pour déterminer comment un fluide visqueux s'écoule dans un tuyau droit.
Son but était de comprendre la dynamique de la circulation sanguine chez l'homme sachant que le plasma sanguin se comporte comme un fluide newtonien.
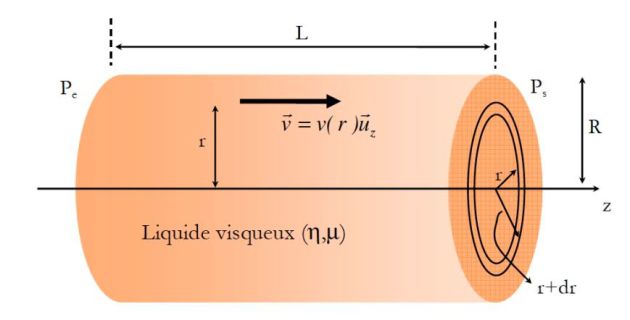
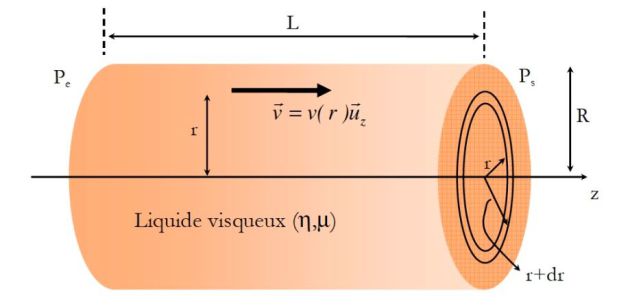
Un fluide visqueux incompressible de densité \(\rho\) s'écoule dans un tube cylindrique de longueur L et de rayon R.
La pression à l'entrée du tube (\(z=0\)) est \(P_E\).
La pression à la sortie du tube est \(P_S\).
On va calculer les champs des vitesses et de pression à l'intérieur du tube en se plaçant en régime stationnaire.
On suppose l'écoulement laminaire :
\(\vec v =v(r) \vec u_z\)
On suppose que \(P=P(r,z)\) (invariance par rotation autour de l'axe Oz) et la pesanteur est négligée.
L'équation de Navier - Stokes s'écrit dans ces conditions :
\(\rho { \left( {\vec v.\overrightarrow {grad} } \right)\vec v}= - \overrightarrow {grad} P + \eta \Delta \vec v\)
On évalue l'accélération convective :
\((\vec v.\overrightarrow {grad} )\vec v = \left( {v(r)\frac{d}{{dz}}} \right)v(r)\vec u_z = \vec 0\)
On obtient ainsi l'équation dite de Stokes :
\( \overrightarrow {grad} P = \eta \Delta \vec v\)
En projection sur \(\vec u_r\) :
\(\frac{{\partial P(r,z)}}{{\partial r}} = 0\)
Par conséquent, la pression ne dépend que de z : \(P(z)\).
En projection selon \(\vec u_z\) :
\(\frac{{dP(z)}}{{dz}} = \eta \frac{1}{r}\frac{d}{{dr}}\left( {r\frac{{dv(r)}}{{dr}}} \right)\)
Le terme de gauche ne dépend que de z alors que le terme de droite ne dépend que de r. Par conséquent :
\(\frac{{dP(z)}}{{dz}} = C \; \; \; \; \;et \; \; \; \; \;\eta \frac{1}{r}\frac{d}{{dr}}\left( {r\frac{{dv(r)}}{{dr}}} \right)=C\)
Où \(C\) est une constante.
Ainsi :
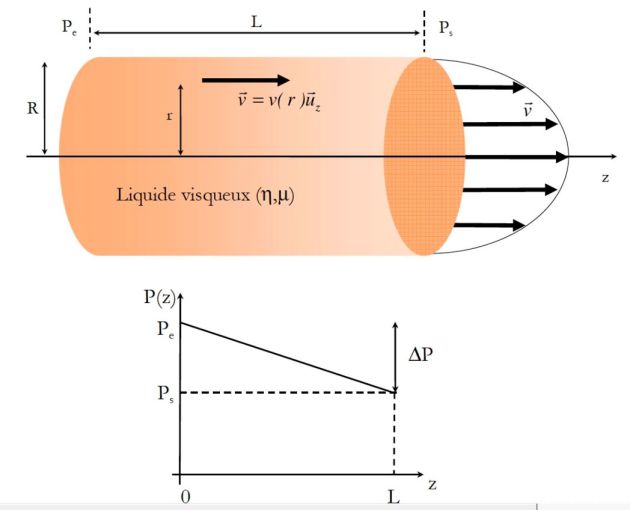
\(P(z) = P_e - \frac{{P_e - P_s }}{L}z = P_e - \frac{{\Delta P}}{L}z\;\;\;\;\;\;\;\;\;\left( {C = - \frac{{\Delta P}}{L}} \right)\)
La vitesse vérifie l'équation différentielle :
\(\eta \frac{1}{r}\frac{d}{{dr}}\left( {r\frac{{dv(r)}}{{dr}}} \right)= - \frac {\Delta P}{L}\)
Après une double intégration et en éliminant le terme qui diverge en \(r=0\), on obtient, en utilisant les conditions aux limites (vitesse du fluide nulle en \(r=R\)) :
\(v(r)=\frac {\Delta P}{4 \eta L}(R^2-r^2)\)
La courbe ci-dessus donne le profil parabolique du champ des vitesses ainsi que la variation affine de la pression.
On appelle "perte de charge" la quantité \(\Delta P=P_E-P_S\).
Méthode : Débit volumique
Le débit volumique vaut ici :
\(D_v = \int_0^R {v(r)2\pi rdr} = \int_0^R {\frac{{\Delta P}}{{4\eta L}}(R^2 - r^2 )2\pi rdr}\)
Soit :
\(D_v = \frac{{\Delta P}}{{\eta L}}\frac{\pi }{8}R^4\)
On définit une "résistance hydraulique", par analogie avec une résistance ohmique (\(\Delta U=V_1-V_2=RI\)) :
\(\Delta P=P_E-P_S=R_{hyd}D_v\)
Soit :
\(R_{hyd}=\frac {8\eta L}{\pi R^4}\)
La résistance hydraulique est d'autant plus élevée que la viscosité du fluide est grande et que le rayon du tube est petit.
Exemple : Perte de charge et résistance hydraulique
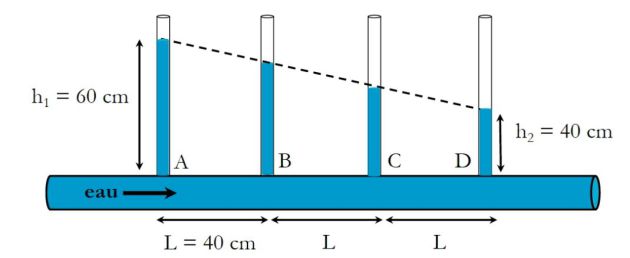
On place une succession de tubes verticaux le long de la conduite.
La mesure des hauteurs d'eau permet de déterminer la perte de charge :
\(\Delta P=\mu _{eau} g (h_1-h_2)=2.10^3\;Pa\)
Si le débit est \(D_v=10\;cm^3.s^{-1}=10^{-5}m^3.s^{-1}\), on peut en déduire la résistance hydraulique :
\(R_{hyd}=\frac {\Delta P}{D_v}=2.10^8Pa.s.m^{-3}\)