Optique ondulatoire ("Classe inversée", PC*)

White light contains all the visible spectrum radiation from \(0,4\) \(\mu m\) (violet) to about \(0,8\) \(\mu m\) (red).

Since there is no interference between sources of different frequencies is obtained on the screen superposition phenomena corresponding to the different wavelengths.

So are the illuminations that will be added.

For a given wavelength \(\lambda_0\) the intensity is at a point \(M\), in the case of Young slits for example :

\(I(M)=2I_0(1+cos(2\pi\frac{ax}{\lambda_0 D})\)

The inter-fringe depends on the wavelength in vacuum :

\(i_{frange}=\frac {\lambda_0 D}{a}\)

• In the center of the interference pattern, the path difference is zero, regardless of wavelength : there is a fringe "zero order" bright and achromatic.

• This bright fringe is bordered by two dark fringes.

• The inter-fringe is minimum for purple and maximum for red : the further away from the center, the more the shift of fringe systems.

  The following two bright fringes are iridescent, purple edge being turned towards the fringe of order \(0\).

When \(x=0\), the intensity is maximum, regardless of the wavelength \(\lambda_0\) : it is thus a bright white fringe.

When further away from the center, the fringes corresponding to the different wavelengths are more and more shifted ; very colorful fringes are observed ("Les couleurs de Newton", in french).

In the vicinity of the points where the intensity of the yellow is zero, the dominant color is purple (mixture of blue and red). The color varies very quickly ; it is said that the color is sensitive.

When one moves further away from the center of the screen, the fringes disappear ; the screen is uniformly illuminated in white (known as white higher order).

The bright fringes of certain wavelengths occupy the same place as the dark fringes of other wavelengths.

If we analyze this light with a spectroscope, it appears black lines corresponding to wavelengths for which there is a dark fringe appear.

Note :

Yellow is the color for which the sensitivity of the eye is maximum.

The process is growing gradually as one moves away from the center; we finally get interference fringes and there is a " white of higher order" (dirty white, much less bright than the achromatic fringe).

If there is a point of abscissa \(x\) of this white of higher order with a spectroscope, we find that on a colored background (rainbow) appear black grooves corresponding to the missing wavelengths : they are those for which the interference is destructive, that is to say for which we have :

\({\varphi _{2/1}} = \frac{{2\pi ax}}{{{\lambda _0}D}} = (2k + 1)\pi\)

We speak of "channeled spectrum".

Examples :

There is a slit in M (\(x = 5\) \(mm\)) and a prism is put at the exit.

Without prism, we see nothing but uniform, apparently white light.

With prism, the various colours are dispersed on a screen.

The rainbow produced by the white light is not uniform : it contains dark fringes, showing that the spectrum of the light has been changed (channeled spectrum)

(\(a = 1,5\) \(mm\) ; \(D = 1,5\) \(m\))

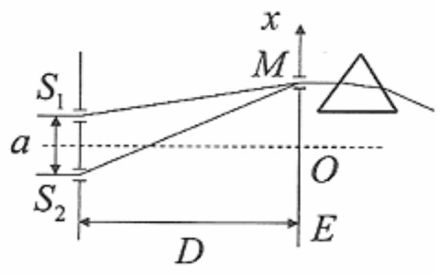
The path length difference is :

\(\delta = \frac{{ax}}{D} = 5\;\mu m\)

Condition to have dark fringes : (destructive interferences)

\(\delta = \frac{{ax}}{D} = 5\;\mu m = (m + \frac{1}{2}){\lambda _0}\;\;\;\;\;\;\;({\lambda _0}\; \in \;\left[ {0,4\;\mu m,0,8\;\mu m} \right]\)

For :

\({\lambda _0} = 0,4\;\mu m\;\;\;\;\; \Rightarrow \;\;\;\;\;m + \frac{1}{2} = 12,5\;\;\;\;\;hence\;\;\;\;\;m = 12\)

The different wavelengths given dark fringes are :

We can see 7 dark fringes.