Détente d'un fluide en régime stationnaire
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
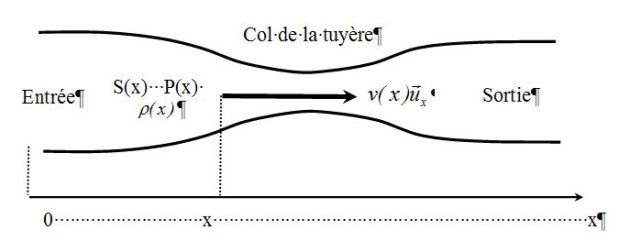
On considère l'écoulement stationnaire dans une tuyère d'un fluide compressible et de vitesse importante.
L'écoulement est supposé irrotationnel.
La section de la tuyère \(S(x)\) est lentement variable avec l'abscisse x. La pression est \(P(x)\), la masse volumique \(\rho (x)\) et la vitesse \(\vec v(x)=v(x)\vec e_x\).
Question
Écrire l'équation d'Euler et la simplifier en tenant compte des hypothèses du texte et en négligeant le poids.
Solution
Compte tenu des hypothèses, l'équation d'Euler devient :
\(\frac{1}{2}\vec {grad} (v^2)=-\frac{1}{\rho} \vec {grad}(P)\)
Question
On considère une variation \(dx\) de l'abscisse du point d'étude.
La pression varie alors de \(dP\), la vitesse de \(dv\) et la masse volumique de \(d\rho\).
Écrire une relation entre \(v\), \(dv\), \(\rho\), \(d\rho\) et \(c\) (vitesse du son dans le fluide).
Solution
L'équation d'Euler s'écrit :
\(\frac{1}{2}\frac{d}{{dx}}({v^2})\,{\vec e_x} = - \frac{1}{\rho }\frac{{dP}}{{dx}} \vec e_x\)
Par conséquent :
\(v\frac{{dv}}{{dx}} = - \frac{1}{\rho }\frac{{dP}}{{dx}}\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;vdv = - \frac{{dP}}{\rho }\)
Question
On rappelle que la vitesse du son \(c\) vérifie la relation :
\(c^2=\frac{dP}{d\rho}\)
En déduire la relation (1) entre \(v\), \(dv\), \(\rho\), \(d\rho\) et \(c\).
Solution
On remplace \(dP=c^2d\rho\) dans la dernière équation, alors :
\(vdv=-c^2\frac{d\rho}{\rho}\) (équation (1))
Question
Écrire l'expression du débit massique \(D_m\) et indiquer l'hypothèse donnée qui justifie sa conservation.
En déduire la relation (2) entre \(v\), \(dv\), \(\rho\), \(d\rho\), \(S\) et \(dS\).
Solution
Le débit massique est :
\(D_m=\rho Sv\)
L'équation de conservation de la masse montre que \(D_m\) est constant en régime stationnaire.
La différentielle logarithmique de l'expression précédente donne :
\(\frac{{d\rho }}{\rho } + \frac{{dS}}{S} + \frac{{dv}}{v} = 0\) (équation (2))
Question
Montrer, à partir des relations (1) et (2) que \(dS/S\) et \(dv/v\) vérifient la relation (3) :
\(\frac{dS}{S}=-f(v)\frac{dv}{v}\)
où \(f(v)\) est une fonction de \(v\) à préciser.
Solution
On élimine \(d\rho /\rho\) entre les équations (1) et (2) :
\(\frac{{dS}}{S} = - \left( {1 - \frac{{{v^2}}}{{{c^2}}}} \right)\frac{{dv}}{v}\;(3)\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;f(v) = - \left( {1 - \frac{{{v^2}}}{{{c^2}}}} \right)\)
Question
En exploitant la relation (3), indiquer comment évolue la vitesse dans les deux parties de la tuyère (avant et après le col) si \(v<c\) et si \(v>c\).
A quelle condition le fluide subit-il une accélération pendant toute la traversée de la tuyère ?
Solution
On suppose \(v<c\) : alors \(f(v)>0\) (écoulement subsonique)
Si \(dS/dx<0\) : \(S(x)\) diminue et \(dv>0\), la vitesse augmente (accélération)
Si \(dS/dx>0\) : \(S(x)\) augmente et \(dv<0\), la vitesse diminue (freinage)
On suppose \(v>c\) : alors \(f(v)<0\) (écoulement supersonique)
Si \(dS/dx<0\) : \(S(x)\) diminue et \(dv<0\), la vitesse diminue (freinage)
Si \(dS/dx>0\) : \(S(x)\) augmente et \(dv>0\), la vitesse augmente (accélération)
Si le fluide atteint la vitesse \(c\) dans le col, il continuera à être accéléré en sortie.
Question
Donner l'expression du débit volumique \(D_v\) du fluide.
Montrer que ce débit est conservé dans le cas où \(v<<c\). Comment peut-on alors considérer l'écoulement ?
Solution
Le débit volumique est :
\(D_v=Sv\)
On calcule la différentielle logarithmique :
\(\frac{{d{D_v}}}{{{D_v}}} = \frac{{dS}}{S} + \frac{{dv}}{v}\)
Si \(v<<c\), alors l'équation (3) devient :
\( \frac{{dS}}{S} + \frac{{dv}}{v}=0\)
Ce qui montre que le débit volumique se conserve.
Le fluide est alors en écoulement incompressible.