Tube de Pitot
Complément : Influence de l'orientation de l'ouverture d'un tube
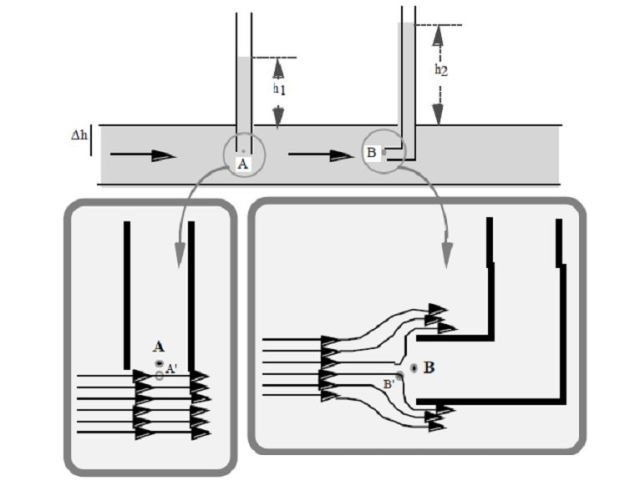
On place deux tubes dans un écoulement liquide, comme précisé sur la figure.
En A', la vitesse est celle de l'écoulement, notée \(v\).
En B', le fluide est immobile et aucune ligne de courant ne passe.
Il y a continuité de pression entre les points A et A' et entre les points B et B'.
Le théorème de Bernoulli et le principe fondamental de la statique des fluides donne :
\(\frac{1}{2}\rho v^2 + P_A = P_B \;\;\;\;\;\;\;\;\;\;et\;\;\;\;\;\;\;\;\;\;P_{atm} = P_A - \rho gh_1 = P_B - \rho gh_2\)
Par conséquent, la vitesse de l'écoulement est :
\(v = \sqrt {2g(h_2 - h_1 } )\)
Le choix de l'orientation des tubes permet donc, par une mesure de dénivellation, d'en déduire la vitesse du fluide.
Fondamental : Sonde Pitot
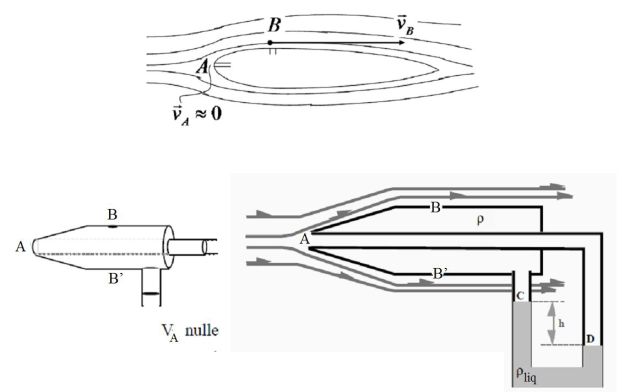
On place un obstacle dans un écoulement d'air (voir figures).
On mesure la pression en un point A situé face à l'écoulement et en un point B situé sur le côté.
Le théorème de Bernoulli donne, en négligeant \(\rho gz\) :
\(\rho \frac{{v_A^2 }}{2} + P_A = \rho \frac{{v_B^2 }}{2} + P_B\)
Or, la vitesse en A est nulle.
On obtient ainsi :
\(v_B = \sqrt {\frac{{2(P_A - P_B )}}{\rho }}\)
Ainsi, la mesure statique de la différence de pressions \( (P_A-P_B) \) permet d'accéder à la mesure de la vitesse au point B, sachant que (on suppose ici que \(\rho_{liq}>>\rho\)) :
\(P_A - P_B = P_D - P_{B'} = P_D - P_C = \rho _{liq} gh\)
Il vient :
\(v_B = \sqrt {2gh\frac{{\rho _{lid} }}{\rho }}\)