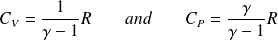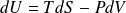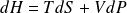To test the understanding of the lesson
Question
Give the differential expression of mass internal energy of an ideal gas.
Give the differential expression of mass internal enthalpy of an ideal gas.
What is the integral expression of the entropy of an ideal gas in terms of the
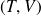 and
and
 variables ?
variables ?
Differential of mass internal energy of a perfect gas :

Differential of the mass internal enthalpy of an ideal gas :
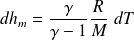
Molar entropy of an ideal gas in terms of the variables
 then
then
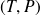 :
: 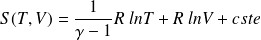
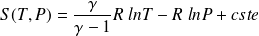
Question
What is the differential expression of the elementary work pressure forces received by a closed system in the general case and in the case of a reversible transformation ?
In the general case, noting
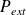 :
:

If the transformation is reversible,
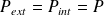 and :
and :

Question
What is the work received by one mole of an ideal gas in a reversible isothermal transformation ?
If the transformation is reversible isotherm :

And :
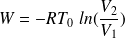
In the case of an expansion,
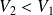 and
and
 : the external environment gets back work.
: the external environment gets back work.
Question
Give the ideal gas equation of state in intensive variables
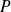 ,
,
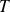 and
and
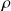 (density).
(density).Give the equation of state of an ideal gas using the Boltzmann constant
 and particle density
and particle density
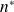 .
.What is the gas state equation of Van der Waals for
 moles, in variables
moles, in variables
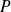 ,
,
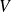 and
and
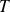 ?
?
Ideal gas equation of state in intensive variables
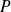 ,
,
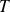 and
and
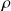 :
: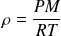 (
(
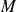 is the molar mass)
is the molar mass)
Equation of state of an ideal gas using the Boltzmann constant and particle density
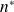 :
: 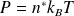
Gas state equation of Van der Waals for
 moles, in variables
moles, in variables
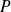 ,
,
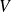 and
and
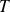 :
: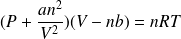
Question
What is an ideal gas ?
At the macroscopic scale : a perfect gas is a (real !) gas studied at low pressures (less than a few bars,
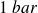 is normal atmospheric pressure).
is normal atmospheric pressure).At the microscopic scale : the particles of an ideal gas are punctual and do not interact with each other but only with the wall of the container they occupy during elastic collisions.
Question
Give the value of the quadratic (RMS) speed of a perfect mono-atomic gas. What is its order of magnitude ?
The root mean square velocity of a perfect mono-atomic gas :
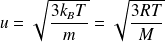
Where
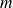 is the mass of a particle,
is the mass of a particle,
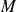 the molar mass,
the molar mass,
 the Boltzmann constant and
the Boltzmann constant and
 perfect gas constant.
perfect gas constant.
Order of magnitude :
For Argon, at
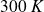 ,
,
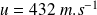 .
.
For Helium, at
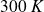 ,
,
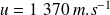 .
.
Question
Express molars capacity
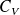 and
and
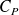 of an ideal gas in terms of
of an ideal gas in terms of
 (gas constant) and
(gas constant) and
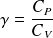 .
.
Question
Give the differential formulation of the first law of thermodynamics for a closed system in its most general form.
Noting
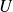 the internal energy,
the internal energy,
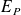 macroscopic gravitational potential energy and
macroscopic gravitational potential energy and
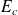 the macroscopic kinetic energy :
the macroscopic kinetic energy :
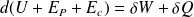
Where
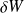 and
and
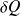 are the work and heat transfer received by the closed system.
are the work and heat transfer received by the closed system.
Question
Give the differential formulation of the second law of thermodynamics for a closed system (system macroscopically at rest).
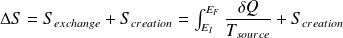
With :
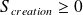
Question
Give the first thermodynamic identity, in differential form ( relationship between
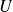 ,
,
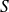 ,
,
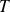 ,
,
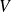 and
and
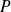 ).
).
Question
Leave the second thermodynamic identity, in differential form (relationship between
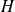 ,
,
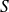 ,
,
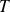 ,
,
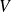 and
and
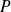 ).
).
Question
How to calculate heat transfer during a transformation at a constant volume ?
How to calculate heat transfer during a transformation at constant external pressure ?
A constant volume :
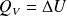
A constant external pressure :
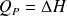
Question
To state the theorem of Carnot on ditherme machines.
Note
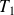 and
and
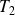 the temperatures of the cold source and the hot source.
the temperatures of the cold source and the hot source.
For a dithermal machine operating irreversibly, the yield is still lower than that obtained during a reversible operation :
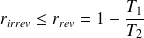
Question
Give the relationship between
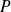 and
and
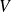 , and between
, and between
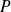 and
and
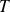 , and finally between
, and finally between
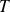 and
and
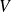 for isentropic evolution of an ideal gas of constant ratio
for isentropic evolution of an ideal gas of constant ratio
 .
.
They write the laws of Laplace :
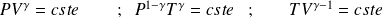
Question
State the "first industrial valid law" for flowing fluids in industrial machines.
Using mass quantities :
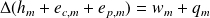
Question
What is the statistical interpretation of entropy ?
Entropy is related to the molecular disorder. The greater entropy of a system, the more disorder.
Thus, the entropy of a pure substance from a liquid to a gaseous state increases.
Question
An electronic pulse generator emits pulses of energy
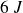 , each at the frequency of
, each at the frequency of
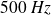 .
.
The efficiency of the generator is equal to
 %.
%.
How many liters of water per minute does it circulate in the cooling system of the generator so that the water temperature at the output does not increase by more than
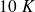 ?
?
The specific heat capacity of water is :
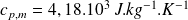 .
.
In a period
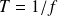 , energy given par the generator is
, energy given par the generator is
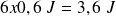 .
.
For the water :

So :
 .
.