Energy study of sound waves
Fondamental : Equation of local conservation of sound energy
Summing the equation : (see the lesson "Acoustic waves")
\(- \mu _0 \frac{{\partial \vec v}}{{\partial t}} = \overrightarrow {grad} p\)
multiplied by the velocity \(\vec v\) and the equation :
\(div(\vec v) = - \chi _S \frac{{\partial p}}{{\partial t}}\)
multiplied by the pressure \(p\).
It comes :
\(pdiv(\vec v) + \vec v.\overrightarrow {grad}(p) = div(p\vec v) = - \mu _0 \vec v.\frac{{\partial \vec v}}{{\partial t}} - \chi _S p\frac{{\partial p}}{{\partial t}} = - \frac{\partial }{{\partial t}}\left( {\frac{1}{2}\mu _0 v^2 + \frac{1}{2}\chi _S p^2 } \right)\)
Let :
Volume density of sound energy :
\(e=\frac{1}{2}\mu _0 v^2 + \frac{1}{2}\chi _S p^2\)
The first term refers to the density of kinetic energy of the fluid and the second the potential energy density associated with the pressure forces.
The vector surface density of sound power :
\(\vec \Pi = p\vec v\)
So :
\(div (\vec \Pi)+\frac{\partial e}{\partial t}=0 \)
One recognizes an equation of type "local energy conservation", already seen for example for the energy of an electromagnetic field or for the conservation equation of energy in the case of thermal conduction phenomena.
Attention : Equation of local conservation of sound energy
\(div (\vec \Pi)+\frac{\partial e}{\partial t}=0 \)
With :
\(e=\frac{1}{2}\mu _0 v^2 + \frac{1}{2}\chi _S p^2\;\;\;\;\;\;and\;\;\;\;\;\;\vec \Pi=p\vec v\)
Complément : Case of a progressive plane wave
Energy densities :
Consider a HPPW which propagates in the direction of \(x>0\). So \(p=\mu_0c_sv\).
So :
\(e_c=\frac {1}{2}\mu_0 v^2=\frac {1}{2}\mu_0 (\frac {p}{\mu_0c_s})^2\)
But :
\(c_s^2=\frac{1}{\mu_0 \chi_S}\)
Whence :
\(e_c=\frac{1}{2}\mu_0v^2=\frac{1}{2}\chi_S p^2=e_p\)
Thus, for a HPPW, densities of kinetic and potential energies are equal.
The density of total energy is then :
\(e=e_c+e_p=\mu_0v^2=\chi_S p^2\)
Vector surface density of sound power :
\(\vec \Pi = p\vec v=\mu_0cv^2\vec u_x\;\;\;\;\;so\;\;\;\;\;\vec \Pi=ce\vec u_x\)
Speed of Energy :
Consider a sound pipe of cross section \(S\) and we will calculate two different ways the energy flowing through the cross section during the time interval \(dt\).
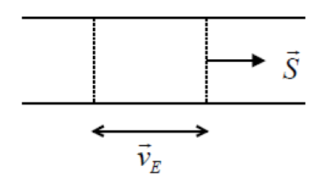
Energy can be calculated from the flux of the vector \(\vec \Pi\) :
\(dE=\iint_S \vec \Pi .d\vec S\; dt=\vec \Pi \vec S\; dt=c_seS\;dt\)
It can be calculated saying it was contained in the volume \(v_ESdt\) :
\(dE=(v_ESdt)e\)
Equating these two expressions that are obtained :
\(v_E=c_s\)
We find the same result as the electromagnetic waves in vacuum, for which the speed of energy is equal to the speed of wave propagation in a vacuum, is \(c\).
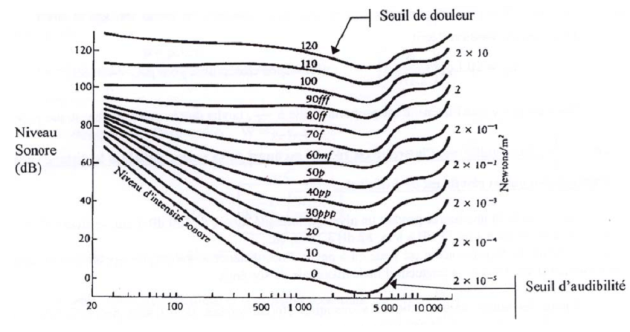
Définition : Sound Intensity
The sound auditory sensation (or sound intensity) depends on the frequency spectrum, duration and especially the intensity of sound.
In general, the intensity of an elastic wave is proportional to both the square of the frequency and the square of the amplitude.
In terms of sound pressure, the sound intensity is proportional to the square of the amplitude \(P_0\) of the pressure wave.
The intensity of natural sounds varies enormously and the human ear is sensitive to a wide range of variation in intensity.
One can support intensities up about \(1\;W.m^{-2}\), which is such a strong sound that begins to hear no more ; it is the pain threshold and corresponds to a sound pressure of only about \( 10\; Pa\).
At the other extreme, the ear detects just the sounds of intensity as low as \(10^{-12}\;W.m^{-1}\).
This is the threshold of audibility, which is associated with a sound pressure of the order of \(10^{-5}\;Pa\).
Rayleigh showed that at \(1 \;kHz\), this corresponds to a sound pressure vibration of the air molecules on the order of \(10^{-6}\;mm\) only.
The human ear operates over a wide range corresponding to a factor of a million (from \(10^{-5}\;Pa\) to \(10\;Pa\)) for pressure and a factor equal to the square of this quantity for sound intensity, is \(10^{12}\).
This is a very broad operating range for a detector.
It is equivalent to that of a device capable of measuring both the diameter of an atom and the length of a football field.
The figure shows the limits of the sensitivity of the ear in function of frequency.
When listening to two sounds, to judge their relative volume, not by the difference of the intensities but by the ratio of the intensities.
An increase in the intensity of sound by the factor of \(10\) is generally seen as a multiplication of the volume by \(2\).
And an intensity sound \(10^{-8}\;W.m^{-2}\) is perceived as twice stronger than its intensity \(10^{-9}\;W.m^{-2}\) and \(0,1\;W.m^{-2}\) is perceived as twice louder than \(0,01\;W.m^{-2}\).
This is equivalent to saying that the ear is sensitive to the logarithm of the intensity.
We define the sound intensity (or acoustic) in decibels (\(dB\)) :
\(I_{dB} = 10\;\log \left( {\frac{{\left\langle \Pi \right\rangle }}{{\left\langle {\Pi _{ref} } \right\rangle }}} \right)\;\;\;\;\;\;\;\;\;\;\left( {with\;:\;\left\langle {\Pi _{ref} } \right\rangle = 10^{ - 12} \;W.m^{ - 2} } \right)\)
\({\left\langle {\Pi _{ref} } \right\rangle }\) corresponds to the hearing threshold for a reference frequency of \(1\;000 \;Hz\).
The pain threshold corresponds approximately to a sound level of \(120 \;dB\).
Some orders of magnitude :
silent room : \(30 \;dB\)
quieter dishwasher : \(50 \;dB\)
Busy street : \(75 \;dB\)
School canteen : \( 100 \; dB\)
Plane : \(120 \;dB\)
Nightclub : \(130 \; dB\)
Rocket : \(180 \;dB\)