Waves in a string
Fondamental : Transverse vibrations of a string ; d'Alembert's wave equation
Consider an inextensible rope, linear density \(\mu\), stretched horizontally with a constant force \(F\).
At equilibrium, the cord is horizontal.
It is assumed in the following that gravity is not involved (if not, the shape of the rope is a chain).
We will study the small movements in the vicinity of this equilibrium, with the following model :
The element of rope located at coordinates \((x,0)\) at equilibrium is at coordinates \((x,y(x,t))\) at non equilibrium. Alternately, we can say we neglect its displacement along (Ox).
The angle \(\alpha (x,t)\) created by the tangent to the rope at the point of abscissa \(x\) at time \(t\) is infinitely small (\(cos \alpha \approx 1\), \(sin \alpha \approx \alpha\) and \(tan \alpha \approx \alpha\), see figure).
If we consider a fictitious cut at the point abscissa \(x\), the action of the left side of the rope on the right is reduced to a tangential force to the rope noted \(\vec T_g(x,t)\).
Similarly, the action of the right on the left side reduces to a force \(\vec T_d(x,t)\).
According to the principle of reciprocal actions, \(\vec T_d(x,t)=-\vec T_g(x,t)\).
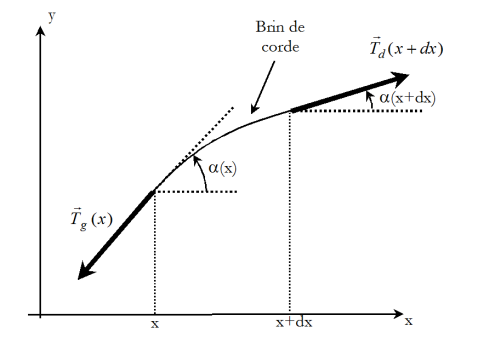
The Newton's second law applied to a rope element located between the abscissas \(x\) and \(x+dx\) gives :
\(\mu \;dx\;\frac{{\partial ^2 y(x,t)}}{{\partial t^2 }}\;\vec u_y = \vec T_g (x,t) + \vec T_d (x + dx,t) = - \vec T_d (x,t) + \vec T_d (x + dx,t)\)
In projection, and noting \(T = \left\| {\vec T_d } \right\|\) :
\(\left\{ \begin{array}{l}0 = - T(x,t)\cos \alpha (x,t) + T(x + dx,t)\cos \alpha (x + dx,t)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1) \\\mu \;dx\;\frac{{\partial ^2 y(x,t)}}{{\partial t^2 }} = - T(x,t)\sin \alpha (x,t) + T(x + dx,t)\sin \alpha (x + dx,t)\;\;\;\;\;\;\;\;\;(2) \\\end{array} \right.\)
If we limit ourselves to the order \(1\), equation \((1)\) provides :
\(T(x + dx) = T(x) = cste = F\)
Equation \((2)\) can be rewritten :
\(\mu \;dx\;\frac{{\partial ^2 y(x,t)}}{{\partial t^2 }} = - F\alpha (x,t) + F\alpha (x + dx,t) = F\;\frac{{\partial \alpha(x,t) }}{{\partial x}}\;dx\)
Yet :
\(\tan \alpha(x,t) = \frac{{\partial y(x,t)}}{{\partial x}} \approx \alpha(x,t)\)
Where :
\(\mu \;\frac{{\partial ^2 y(x,t)}}{{\partial t^2 }} = F\;\frac{{\partial ^2 y(x,t)}}{{\partial x^2 }}\;\;\;\;\;\;\;so\;\;\;\;\;\;\frac{{\partial ^2 y(x,t)}}{{\partial x^2 }} - \frac{1}{{c^2 }}\frac{{\partial ^2 y(x,t)}}{{\partial t^2 }} = 0\;\;\;\;\;\;\;(with\;c = \sqrt {\frac{F}{\mu }} )\)
We find again the d'Alembert's wave equation.
In the case of the rope, the wave is called transverse (displacement occurs along \((Oy)\) axis).
Attention : Wave equation d'Alembert
\(\mu \;\frac{{\partial ^2 y(x,t)}}{{\partial t^2 }} = F\;\frac{{\partial ^2 y(x,t)}}{{\partial x^2 }}\;\;\;\;\;\;\;so\;\;\;\;\;\;\frac{{\partial ^2 y(x,t)}}{{\partial x^2 }} - \frac{1}{{c^2 }}\frac{{\partial ^2 y(x,t)}}{{\partial t^2 }} = 0\)
We find a d'Alembert's wave equation.
The wave propagation speed is :
\(c = \sqrt { \frac {F}{\mu}}\)
The tighter the rope and the lighter the rope weight are, the greater the speed is.
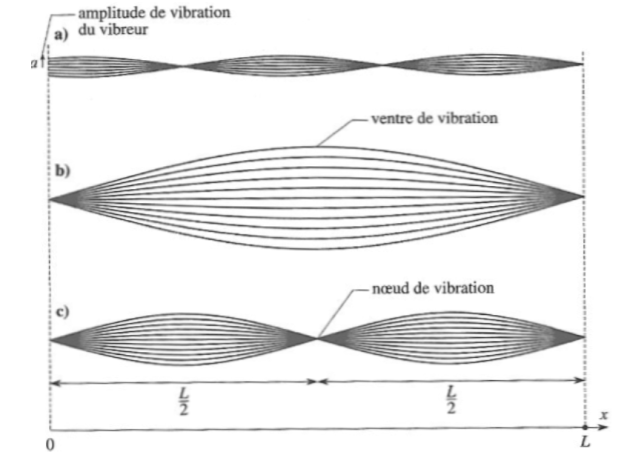
Fondamental : The string Melde
In the experience of Melde, the extremity abscissas \(x=L\) of a rope is fixed (\(y(L,t)=0\)) and operator imposes at \(x=0\) a harmonic movement :
\(y(0,t)=a cos( \omega t)\)
The angular frequency is \(\omega\).
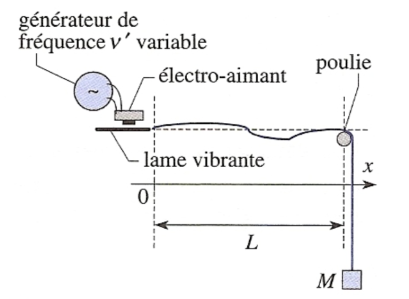
We are interested in forced regime (driven vibration), obtained after disappearance of the transitional regime.
It is thus sought a solution of the d'Alembert equation corresponding to a standing wave of as the same angular frequency as of that of the exciter :
\(y(x,t) = Ccos \left( {kx - \psi } \right)cos \left( {\omega t - \varphi } \right)\)
The boundary conditions needed :
\(y(0,t) = Ccos \left( \psi \right)cos \left( {\omega t - \varphi } \right) = acos (\omega t)\)
And :
\(y(L,t) = 0 = Ccos \left( {kL - \psi } \right)cos \left( {\omega t - \varphi } \right)\)
Whence :
\(a = Ccos \left( \psi \right)\;\;;\;\;\varphi = 0\;\;;\;\;kL - \psi = \frac{\pi }{2}\)
Is :
\(C = \frac{a}{{\sin (kL)}}\;\;\;;\;\;\varphi = 0\;\;\;;\;\;\psi = kL - \frac{\pi }{2}\)
Therefore :
\(y(x,t) = a\;\frac{{\sin \left( {k(L - x)} \right)}}{{\sin (kL)}}\;\cos \omega t\;\;\;\;\;\;\;(with\;k = \frac{\omega }{c})\)
The amplitude is maximum for :
\(sin(k(L-x))=\pm 1\)
And is, in absolute value :
\(y_{max}=\left| {\frac {a}{sin(kL)}} \right|\)
This maximum amplitude becomes infinite (the rope is then in resonance) to excitatory pulses such as :
\(kL = n\pi \;\;\;\;\;so\;\;\;\;\;\omega _n = n\frac{{\pi \;c}}{L}\)
corresponding to the eigen-modes of the string.
However, the inevitable damping and stiffness of the rope make the maximum amplitude keeps a finite value.
Thus stationary wave becomes resonant (in driving regime) when the driving angular frequency coincides with a vibrational frequency (open plan) of string vibration, just like a LC series circuit where \(\omega_0=1/\sqrt{LC}\) the angular frequency of vibration refers to the own frequency of free regime (free oscillation) and the angular frequency of resonance in forced regime (forced oscillation).