Lloyd mirror
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
Consider a parallel beam of polarized light perpendicular to the plane of incidence on a plane mirror.
The source is monochromatic, in the field of infrared IR : \(\lambda=500\;\mu m\).
An IR detector placed on an axis (Oz) perpendicular to the plane of the mirror, can thus superimposing a direct wave (beam \(1\)) and a reflected wave (beam \( 2\)), while giving a quadratic detection.
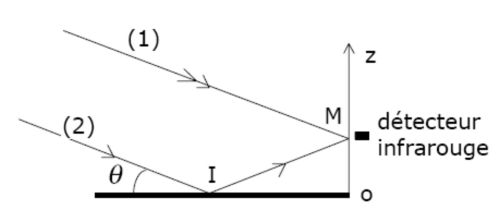
The incident beam forms an angle \(\theta=10°\) with the plane of the mirror.
Question
In this question, the mirror is assumed to be perfectly reflecting.
Recall that the condition should check the electric field at \(z=0\) ; show that the incident wave undergoes a phase shift at the reflection on the mirror equal to \(\pi\).
Indice
The field inside a perfect metal is zero.
Solution
The plane mirror is assumed to be perfect, the electric field is zero in the metal layer.
The tangential component of the electric field is still ongoing and the field here is purely tangential (polarization perpendicular to the plane of incidence), the total field will be null at \(z=0\).
Therefore :
\(\vec E_i + \vec E_r = \vec 0\)
Is :
\(\vec E_r=-\vec E_i\)
Thus, a phase shift in reflection (equal to \(\pi\)).
Question
Determine the order of interference \(p(z)\) at the point \(M\).
What is the shape of the fringes ? Calculate the interfringe.
What is the interest to work in IR ?
Solution
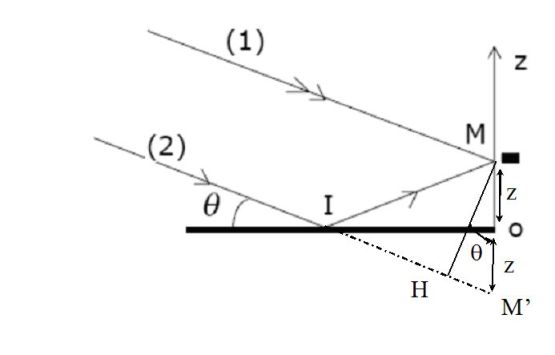
Using the theorem of Malus, the geometric path difference is clear in the figure :
\(\delta_{geo} = HM'=2zsin\theta\)
The overall path length difference, taking into account the reflection on the mirror is :
\(\delta=2zsin\theta + \frac {\lambda_0}{2}\)
And the order of interference in \(M\) becomes :
\(p(z)=\frac {2sin\theta}{\lambda_0}z+\frac{1}{2}\)
The bright fringes are obtained when the order is integer (\(p\) is an integer) :
\(\frac {2sin\theta}{\lambda_0}z+\frac{1}{2}=p\)
The bright fringes are straight line of equation :
\(z_p=\frac{\lambda_0}{2sin\theta}(p-\frac{1}{2})\)
The interfringe is given by :
\(i=z_{p+1}-z_p=\frac{\lambda_0}{2sin\theta}=1,44\;mm\)
Infrared correspond to large wavelengths, which provides well-spaced fringes.
Question
It is now assumed that the coefficient of intensity of the reflection of the mirror is \(R=0,85\).
Calculate fringe contrast and conclude.
Indice
What is the definition of reflection coefficient of energy ?
Use the definition of contrast : \(C=\frac {I_{max}-I_{min}}{I_{max}+I_{min}}\)
Solution
The intensity of the ray that is reflected on the mirror is now \(I_2=RI_0\), where \(I_0\) is the intensity of the first ray which arrives directly at the point M.
Intensity at \(M\) becomes :
\(I(M)=I_0+RI_0+2\sqrt{R}I_0cos(2\pi p(z))\)
The maximum intensity is :
\(I_{max}=I_0+RI_0+2\sqrt{R}I_0\)
And the minimum intensity is :
\(I_{min}=I_0+RI_0-2\sqrt{R}I_0\)
The contrast is deduced :
\(C=\frac {I_{max}-I_{min}}{I_{max}+I_{min}}=\frac{2\sqrt{R}}{1+R}\)
The numerical application gives \(C=99,7\)% : the fringes are well contrasted. The contrast is sensitive to other factors that the reflection coefficient of the mirror.