Équations de Maxwell n°2

Cours

Objectifs
Introduction
Exercice : Condensateur alimenté à haute fréquence
Bilan d'énergie électromagnétique
Exercice : Énergie magnétique stockée dans une bobine
Exercice : Charge d'un condensateur, bilan énergétique
Exercice : Pour tester sa connaissance du cours
Conclusion

Pour tester sa connaissance du cours

Question

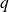Donner le vecteur densité de courant électrique dans un milieu contenant porteurs de charges par unité de volume., se déplaçant à la vitesse .

Solution

Le vecteur densité de courant électrique est :

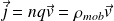
Question

Comment définir l'intensité électrique dans le cas d'un courant volumique puis dans le cas d'un courant surfacique ?

Solution

Courant volumique : l'intensité du courant est le flux du vecteur 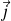à travers une surface S :

Si le vecteur 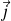est uniforme et perpendiculaire à la surface, .
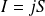Courant surfacique : l'intégrale se réduit alors à une intégrale curviligne :

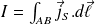
Si le vecteur 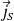est uniforme et perpendiculaire au segment de longueur , .

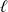Question

Donner l'expression locale du principe de conservation de la charge électrique.

Solution

C'est une équation classique de conservation :

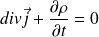
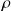est ici la charge volumique totale et non pas seulement la charge volumique mobile 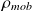qui intervient dans la définition de .

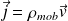Question

Démontrer la loi des nœuds (vue en électricité) en régime stationnaire.

Solution

En régime stationnaire, 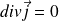. Par conséquent, 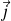est à flux conservatif :

Ou, ce qui revient au même, sur un tube de champ (ou un tube de courant) au niveau d'un nœud :

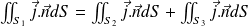
On démontre ainsi la loi des nœuds :

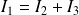
Question

Écrire les 4 équations de Maxwell, dans le cas le plus général.
Comment se simplifient-elles dans un conducteur ohmique ?

Solution

Les équations de Maxwell sont :
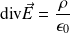(Équation de Maxwell - Gauss, MG)
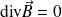(Équation du flux magnétique)
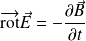(Équation de Maxwell - Faraday, MF)
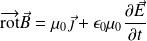(Équation de Maxwell - Ampère, MA)
Dans le cas d'un conducteur ohmique :

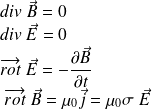
Question

Démontrer le théorème de Gauss à partir de l'équation de Maxwell - Gauss.

Solution

On utilise le théorème de Green-Ostrogradsky :

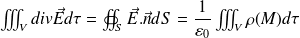
Soit :

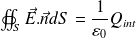
Question

Démontrer le théorème d'Ampère à partir de l'équation de Maxwell - Ampère.

Solution

On utilise le théorème de Stockes :

Soit :

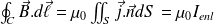
Question

Pourquoi dit-on que le champ magnétique est à flux conservatif ?

Solution

L'équation de Maxwell-Flux, 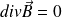, conduit à :

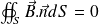
Ce qui signifie que le champ magnétique est à flux conservatif.

Question

Donner l'énergie volumique d'origine électrique d'un champ électromagnétique
Donner l'énergie volumique d'origine magnétique d'un champ électromagnétique

Solution

Énergie volumique d'origine électrique d'un champ électromagnétique :
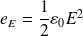
Énergie volumique d'origine magnétique d'un champ électromagnétique :
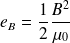
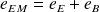est l'énergie volumique totale du champ EM.

Question

Définir le vecteur de Poynting en électromagnétisme, noté .
Donner la puissance volumique reçue par la matière de la part d'un champ EM. Que vaut elle dans le cas d'un milieu ohmique ?
Écrire, en présence de sources de courant volumiques 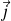, le bilan local puis intégral de l'énergie du champ électromagnétique .

Solution

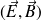Vecteur de Poynting en électromagnétisme :
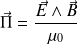
Puissance volumique reçue par la matière de la part d'un champ EM :

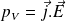
Pour un conducteur ohmique (pour lequel la loi d'Ohm locale est vérifiée, ) :
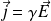Bilan local de conservation de l'énergie EM :

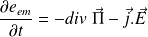
La forme intégrale de la conservation de l'énergie EM est :

Question

Donner l'énergie d'origine magnétique instantanée emmagasinée dans une bobine d'inductance L parcourue par un courant d'intensité i(t).
Quelle est l'énergie magnétique d'un système de deux circuits d'inductances propres respectives L₁ et L₂ et de mutuelle M parcourus par des courants respectifs I₁ et I₂ ?

Solution

Énergie d'origine magnétique instantanée emmagasinée dans une bobine d'inductance L parcourue par un courant d'intensité i(t) :
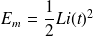
Énergie magnétique d'un système de deux circuits d'inductances propres respectives L₁ et L₂ et de mutuelle M parcourus par des courants respectifs I₁ et I₂ :

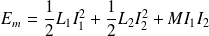
Question

Quelle est l'énergie emmagasinée par un condensateur ?
Définir la capacité d'un condensateur ? Que vaut-elle pour un condensateur plan ?

Solution

Énergie d'origine électrique instantanée emmagasinée dans un condensateur de capacité C soumis à la tension u(t) :
La capacité d'un condensateur est définie par :

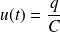
Pour un condensateur plan :

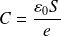
où est la surface des armatures et la distance entre les armatures.
Si un diélectrique de permittivité relative est placé entre les deux armatures, la capacité devient :

Accueil

Imprimer