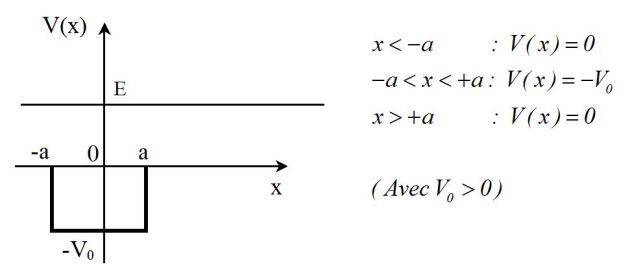Ramsauer effect
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
Question
Schrodinger's time-independent equation is, where \(\varphi (x)\) is the probability amplitude :
\(- \frac{{{\hbar ^2}}}{{2m}}\frac{{{d^2}\varphi (x)}}{{d{t^2}}} + V(x)\varphi (x) = E\varphi (x)\)
Solve this equation in the case of a quantum particle of mass \(m\), placed in an infinite potential well of width \(L\), in order to find the results of the lesson.
Solution
See the lesson : "Particle in an infinite well"
Question
In 1921, physicist Ramsauer noticed that, for some values of the incidental energy, gases like Helium were perfectly transparent to electron beams of low energy.
Let us consider a stationary solution to Schrodinger's equation, of positive energy \(E\) for an electron of mass \(m\) in the potential described by the following picture.
Prove that the probability amplitude \(\varphi (x)\) can be expressed by :
\(\varphi (x) = \left\{ \begin{array}{l}A{e^{ikx}} + \underline B {e^{ - ikx}}\;\;\;\;\;\;\;(x < - a) \\\underline C {e^{iKx}} + \underline D {e^{ - iKx}}\;\;\;\;\;\;( - a < x < + a) \\\underline F {e^{ikx}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(x > a) \\\end{array} \right.\)
\(K\) and \(k\) are parameters to be expressed in function of the given data.
\(A\), \(\underline B\), \(\underline C\), \(\underline D\) and \(\underline F\) are complex constants of integration that we will not try to determine.
Solution
The expressions of \(k\) and \(K\) are :
\(k = \sqrt {\frac{{2mE}}{{{\hbar ^2}}}} \;\;\;\;\;\;\;\;and\;\;\;\;\;\;\;\;\;K = \sqrt {\frac{{2m(E + {V_0})}}{{{\hbar ^2}}}}\)
Question
Write the four equations linking these constants of integration.
Solution
The continuity of the wave function and its derivative in \(+a\) and \(–a\) lead to :
\(\left\{ \begin{array}{l}A{e^{ - ika}} + \underline B {e^{ika}} = \underline C {e^{ - iKa}} + \underline D {e^{iKa}} \\ikA{e^{ - ika}} - k\underline B {e^{ika}} = iK\underline C {e^{ - iKa}} - iK\underline D {e^{iKa}} \\\end{array} \right.\;\;\;\;\;\;\;and\;\;\;\;\;\;\;\left\{ \begin{array}{l}\underline C {e^{iKa}} + \underline D {e^{ - iKa}} = \underline E {e^{ika}} \\iK\underline C {e^{iKa}} - iK\underline D {e^{ - iKa}} = ik\underline E {e^{ika}} \\\end{array} \right.\)
Question
A calculation, which is not asked, leads to the expression of the probability amplitude ratio :
\(\frac{{\underline B }}{A} = \frac{{{k^2} - {K^2}}}{{{{(k + K)}^2} - {e^{4iKa}}{{(K - k)}^2}}}{e^{ - 2ika}}(1 - {e^{4iKa}})\)
Determine the expression of \(R\), the probability of current reflection coefficient of the well of potential that is studied.
What is the value of \(T\), the probability of current transmission coefficient ?
Solution
The coefficient of reflection is :
\(R = {\left| {\frac{{\underline B }}{A}} \right|^2} = \frac{{4{{({k^2} - {K^2})}^2}}}{{16{k^2}{K^2} + 4{{({k^2} - {K^2})}^2}{{\sin }^2}(2Ka)}}{\sin ^2}(2Ka)\)
Coefficient \(T\) is simply equal to :
\(T=1-R\)
Question
How can the Ramsauer effect be interpreted ?
For Helium, the minimum incidental energy for which Ramsauer effect happens is \(E=0,7\) \(eV\).
The radius of the Helium atom is \(a=0,1\) \(nm\).
Compute the value of the depth of the well \(V_0\) inside the atom.
Data :
\(\hbar \approx 10^{-34}J.s\) and \(m\approx 10^{-30}kg\) (mass of the electron)
Solution
Helium is transparent to the electron if \(R = 0\) (or \(T=1\)) : the electron does not see the potential well.
But \(R=0\) is equivalent to :
\(\sin (2Ka) = 0\;\;\;\;\;\;\;so\;\;\;\;\;\;\;Ka = p\frac{\pi }{2}\)
The De Broglie wavelength of the electron inside the well is :
\(\lambda = \frac{{2\pi }}{K}\;\;\;\;\;\;\;so\;\;\;\;\;\;\;2a = p\frac{\lambda }{2}\)
All reflected waves interfere in a destructive manner.
The well comes transparent for the incidental wave.
The reflected wave in \(x = -a\), which does not enter the well, interferes in a destructive way with the waves resulting from multiple reflections.
The energy associated to mode \(p\) is :
\({E_p} = \frac{{{\hbar ^2}{\pi ^2}}}{{8m{a^2}}}{p^2} - {V_0}\)
For \(n=1\), we find \(V_0=8,7\) \(eV\).
Question
Can you give an analogous phenomena to the Ramsauer effect in other subjects of physics ?
Solution
Gel used in ultrasound scan for a better transmission
Anti-noise walls
Anti-reflection glasses