Heisenberg's indeterminacy equations
Fondamental : Heisenberg's space uncertainty principle
At a given time, the measure of the position \(x\) and the quantity of movement \(p_x\) on the \((Ox)\) axis both show fundamental indeterminacies.
These are written \(\Delta x\) and \(\Delta p_x\).
They verify Heisenberg's indeterminacy equation :
\(\Delta x \Delta p_x \ge \frac {\hbar}{2}\)
This inequality shows that a quantum state does not give a perfect knowledge of this state in a classical point of view.
The notion of trajectory disappears in quantum mechanics.

Complément : Heisenberg's indeterminacy principle explains the diffraction of light
Let us consider the diffraction of a light beam by a thin slit of width \(a\).
The photon has travelled through a slit.
We can write :
\(\Delta x \approx a/2\)

Heisenberg's indeterminacy principle gives :
\(\Delta p_x\approx \frac {\hbar}{a}\)

The indeterminacy on the quantity of movement is given by the vertical coordinate :
\(\Delta {p_x} \approx p\sin \theta \approx \frac{h}{\lambda }\sin \theta\)
Hence the diffraction angle :
\(\sin \theta \approx \theta \approx \frac{\lambda }{h}\Delta {p_x}\;\;\;\;\;so\;\;\;\;\;\theta \approx \frac{\lambda }{h}\frac{\hbar }{a} \approx \frac{1}{{2\pi }}\frac{\lambda }{a}\)
The order of magnitude of the angle is the same as the one given by the diffraction theory.
Diffraction can be interpreted thanks to Heisenberg's uncertainty principle.
Exemple : Minimum energy of a particle in an infinite potential well
Let us consider a particle of mass \(m\) in a "quantum box" : the potential energy of the particle is nil in the well (\(L/2<x<+L/2\)) and infinite elsewhere.
The particle cannot exit the potential well.
The maximum indeterminacy on the position of the particle is approximately :
\(\Delta x \approx \frac {L}{2}\)
The indeterminacy principle gives the minimum uncertainty for \(p_x\) :
\(\Delta p_x = p_x\approx \frac {\hbar}{L}\)
The minimum energy of the particle is then :
\(E_{min}=\frac {p_x^2}{2m}\)
So :
\(E_{min} \approx \frac {\hbar ^2}{2mL^2}\)
Heisenberg's inequalities can determine the minimum energy of containment.
Fondamental : Heisenberg's time indeterminacy principle
Let \(\Delta E\) be the indeterminacy on the measure of an energy and \(\Delta t\) the duration of the measure of this energy. Then :
\(\Delta E \Delta t \ge \hbar\)
If the duration of the interaction was nil, then \( \Delta E\) would be infinite and the energy of the particle would not be determined.
Conversely, a fundamental state with an infinite lifetime has a perfectly determined energy.
This inequality asserts that the energy conservation principle cannot be verified. The uncertainty is \(\Delta E\) during a time \(\Delta t\) such as \(\Delta t \approx \hbar / \Delta E\).
With this principle can be explained the concept of virtual particles, messenger of fundamental interactions.
Such a particle of mass \(m\) (and of energy linked to its mass, \(mc^2\)) can exist during a period of time \(\Delta t\) given by the indeterminacy principle :
\(\Delta t\approx \frac {\hbar}{mc^2}\)
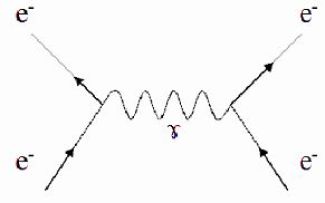
The previous picture shows a Feynman diagram of the interaction between two electrons : the oblique lines represent the moving electrons and the wavy lines represent the virtual exchanged photon.
