Quantum mechanics

The law of the black-body describes its electromagnetic radiation behavior when it is in thermal equilibrium with matter.

It specifies the spectral repartition of total electromagnetic energy density.

Let \(u_{\nu}(\nu)\) be the spectral density, so that the density of electromagnetic energy between the frequencies \(\nu\) and \(\nu +d\nu\) is written :

\(du(\nu)=u_{\nu}d\nu\).

Physicist Planck established at the end of the XIXth century that the spectral density \(u_{\nu}(\nu)\) could be written as :

\({u_\nu }(\nu ) = \frac{{8\pi {\nu ^2}}}{{{c^3}}}\frac{{h\nu }}{{\exp (h\nu /kT) - 1}}\)

The figure below shows the graphs of the curves associated to \(u_{\nu}(\nu)\) at different temperatures.

We establish that these curves all go through a maximum, which depends on temperature, for a frequency \(\nu_{max}(T)\).

It follows Wien's law :

\({\nu _{\max }} = \alpha T\;\;\;\;\;(\alpha = {1,04.10^{11}}{s^{ - 1}}.{K^{ - 1}})\)

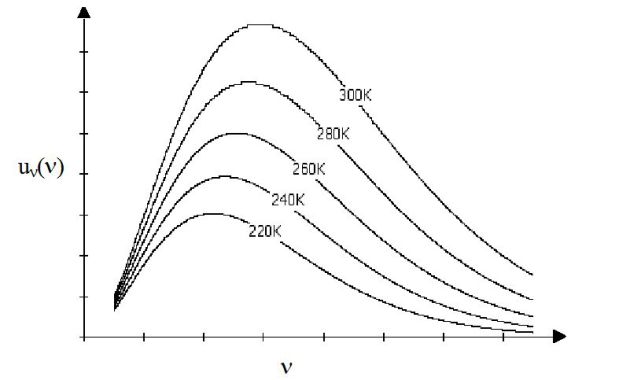
It is remarkable to notice that the spectrum of a black-body radiation is continuous and does not depend on the physical-chemical nature of the latter, but only depends on its temperature.

These properties are a direct consequence of the thermal equilibrium in which the body is.

The emission and absorption spectra of atoms are discontinuous.

When a body is heated, it emits a radiation in its spectrum of emission.

However, the emission and absorption spectra of an atom are identical.

Hence, at thermal equilibrium, atoms located inside the black-body absorb all of the radiation they emit.

There is only one radiation left in the body. It results from its thermodynamic state, and its spectrum is continuous.