Le schéma du filtre passe-bande utilisé peut être le suivant :

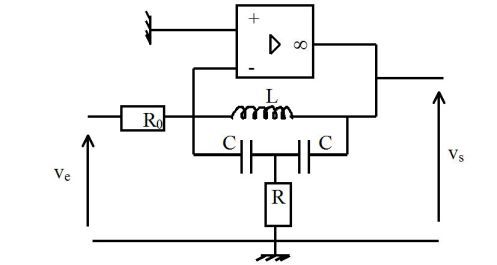
Avec :

\(L=2,2\;mH\;\; ;\;\;C=10\;nF\;\; ;\;\;R_0=22\;k\Omega\;\; ;\;\;R=10\;k\Omega\)

Déterminer expérimentalement (par une méthode rapide) :

• la fréquence de résonance \(f_0\)

• la bande passante \(\Delta f\)

• le facteur de qualité \(Q\)

• le coefficient d'amortissement \(\sigma\) de ce filtre.

On réalise désormais l'analyseur de spectres en branchant les différents blocs les uns à la suite des autres.

Le détecteur de crête est le circuit suivant :

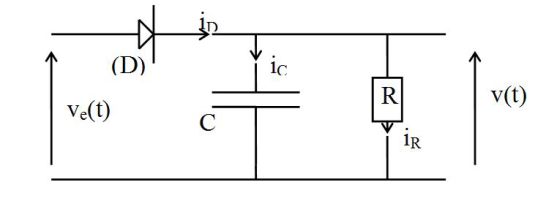
Avec :

\(R=30\;k\Omega\;\; ;\;\;C=100\;nF\)

On regardera le TP sur la modulation d'amplitude pour la théorie du montage "détecteur de crête".

On choisit un signal à analyser carré \(v_1(t)\) de fréquence \(f_1=10\;kHz\) et de valeur maximale \(v_1=2\;V\), délivré par un premier générateur.

La décomposition en séries de Fourier de ce signal est :

\({v_1}(t) = \frac{{4{V_1}}}{\pi }\left[ {\sin 2\pi {f_1}t\mathop {}\limits^{} + \mathop {}\limits^{} \frac{1}{3}\sin 2\pi 3.{f_1}t\mathop {}\limits^{} + \mathop {}\limits^{} \frac{1}{5}\sin 2\pi 5.{f_1}t\mathop {}\limits^{} + \mathop {}\limits^{} ...} \right]\)

On multiplie ce signal par une tension sinusoïdale dont la fréquence dépend du temps (tension vobulée), fournie par un second générateur :

\(u_0(t)=U_0sin(2\pi(f_0+\delta f_0)t)\)

Avec :

\(f_0=50\;kHz\)

et \(\delta f_0\) variant de 0 à 100 kHz (soit une fréquence maximale de 150 kHz) et \(U_0=2\;V\).

Notons \(a_nsin(2\pi f_1 t)\) l'harmonique de rang n du signal carré.

A la sortie du multiplieur, la tension correspondant à cet harmonique sera :

\({s_n}(t) = k{U_0}{a_n}\sin 2\pi ({f_0} + \delta {f_0})t.\sin 2\pi n{f_1}t\)

Soit :

\({s_n}(t) = \frac{{k{U_0}{a_n}}}{2}\left[ {\sin 2\pi \left[ {\left( {{f_0} + \delta {f_0}} \right) - n{f_1}} \right]t\mathop {}\limits^{} - \mathop {}\limits^{} \sin 2\pi \left[ {\left( {{f_0} + \delta {f_0}} \right) + n{f_1}} \right]t} \right]\)

Ce signal, différence de signaux sinusoïdaux de fréquences \(f_0+\delta f_0-nf_1\) et \(f_0+\delta f_0+nf_1\), injecté à l'entrée du filtre passe-bande sélectif de fréquence centrale justement \(f_0\), ne donnera de valeurs significatives en sortie du filtre que lorsqu'une au moins de ces fréquences sera égale à \(f_0\).

Par exemple :

Fondamental (f₁ = 10 kHz) : il faut que δf₀ = 10 kHz.

1^er harmonique (30 kHz) : il faut que δf₀ = 30 kHz

2^ème harmonique (50 kHz) : il faut que δf₀ = 50 kHz

3^ème harmonique (70 kHz) : il faut que δf₀ = 70 kHz

4^ème harmonique (90 kHz) : il faut que δf₀ = 90 kHz

On obtient ainsi, en sortie du filtre passe-bande, des signaux d'amplitudes proportionnelles à a_n (amplitude du fondamental ou des harmoniques de rang n) et de fréquences dépendant du temps de manière linéaire.

• Visualiser tout d'abord, en mode X-Y, la tension à la sortie du filtre passe-bande, en fonction de la tension de wvobulation (tension en dents de scie ou rampe de tension, située à l'arrière du GBF qui vobule).

• Visualiser, toujours en mode X-Y, la tension à la sortie du détecteur de crête en fonction de la tension de wobulation.

  Le détecteur de crête permet alors de ne garder que l'enveloppe des signaux observés.

• Conclure (Comparer notamment les amplitudes respectives du fondamental et des harmoniques observés).

• Choisir un signal triangulaire puis sinusoïdal de fréquence f₁ = 10 kHz.

  Réaliser de même l'analyse spectrale de ces signaux.

  Conclure.