Les machines thermiques
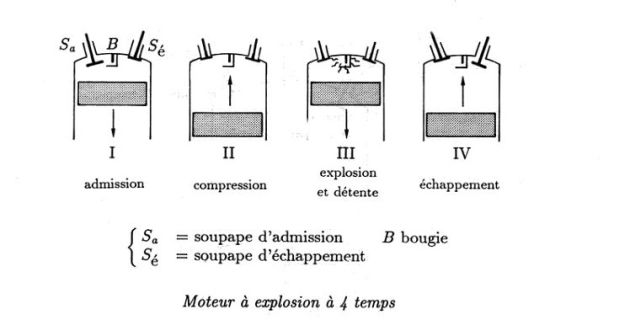
Exemple : Cycle théorique de Beau de Rochas (1862), réalisé par Otto (1876) - le moteur à explosion à 4 temps
Simulation :
Méthode : Étude théorique du cycle de Beau de Rochas - Calcul du rendement
Hypothèses simplificatrices :
Durant le cycle, les propriétés du fluide changent. On n'en tient pas compte et on considère le gaz comme un GP.
C'est toujours le même gaz qui subit le cycle.
Les transformations sont réversibles :
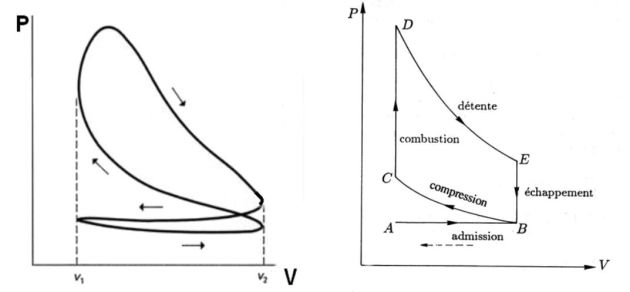
BC : compression adiabatique
CD : isochore (étincelle de la bougie)
DE : détente adiabatique
EB : refroidissement isochore
Rendement du cycle :
Le cycle est moteur (W < 0) : le fluide reçoit de la chaleur lors de la transformation CD et donne de la chaleur au milieu extérieur lors de la transformation EB.
W désigne ici la somme des travaux reçus par le gaz lors du cycle (c'est-à-dire lors des 4 transformations).
Le rendement \(\rho\) du cycle (du moteur) est défini par :
\(\rho = \frac{{travail\;re\c{c}u\;par\;l'exterieur}}{{energie\;calorifique\;fournie}}\)
Soit, ici :
\(\rho = \frac{{( - W)}}{{{Q_{CD}}}} = - \frac{W}{{{Q_{CD}}}}\)
D'après le 1er principe :
\(\Delta U = W + {Q_{CD}} + {Q_{EB}} = 0\)
Soit :
\(W = - {Q_{CD}} - {Q_{EB}}\)
L'expression du rendement devient :
\(\rho = \frac{{{Q_{CD}} + {Q_{EB}}}}{{{Q_{CD}}}} = 1 + \frac{{{Q_{EB}}}}{{{Q_{CD}}}}\)
Or (transformations isochores) :
\(\begin{array}{l}{Q_{CD}} = \Delta {U_{CD}} = n{C_{V,mol}}({T_D} - {T_C}) \\{Q_{EB}} = \Delta {U_{EB}} = n{C_{V,mol}}({T_B} - {T_E}) \\\end{array}\)
D'où :
\(\rho = 1 + \frac{{{T_B} - {T_E}}}{{{T_D} - {T_C}}}\)
Pour les deux isentropiques (adiabatiques réversibles), on peut écrire :
\(\left\{ \begin{array}{l}{T_B}V_B^{\gamma - 1} = {T_C}V_C^{\gamma - 1} \\{T_D}V_D^{\gamma - 1} = {T_E}V_E^{\gamma - 1} \\\end{array} \right.\)
En notant que \(V_A=V_B\) et \(V_D=V_C\), il vient :
\(\left\{ \begin{array}{l}{T_C} = {\left( {\frac{{{V_B}}}{{{V_A}}}} \right)^{\gamma - 1}}{T_B} \\{T_D} = {\left( {\frac{{{V_B}}}{{{V_A}}}} \right)^{\gamma - 1}}{T_E} \\\end{array} \right.\)
On en déduit l'expression du rendement :
\(\rho = 1 + \frac{{{T_B} - {T_E}}}{{{{\left( {\frac{{{V_B}}}{{{V_A}}}} \right)}^{\gamma - 1}}{T_E} - {{\left( {\frac{{{V_B}}}{{{V_A}}}} \right)}^{\gamma - 1}}{T_B}}}\)
Soit, finalement :
\(\rho = 1 - {\left( {\frac{{{V_A}}}{{{V_B}}}} \right)^{\gamma - 1}}\)
On note \(\alpha=V_B/V_A\) le taux de compression :
\(\rho = 1 - {\left( {\frac{1}{\alpha }} \right)^{\gamma - 1}}\)
Pour \(\alpha\) compris entre 8 et 10 et avec \(\gamma=7/5\), \(\rho \approx 0,56\).
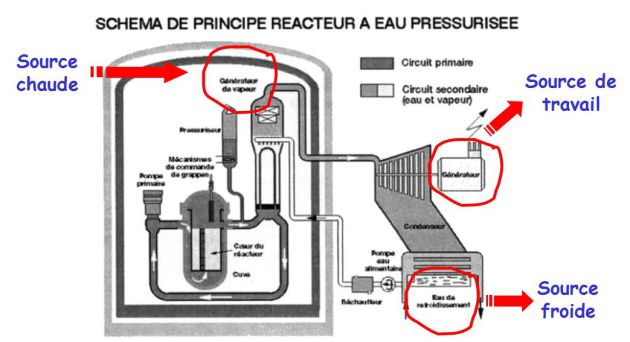
Fondamental : La machine thermique de Carnot
Principe général d'une machine thermique :
La figure suivante donne le principe d'une machine de Carnot (machine ditherme).
Un fluide subit des cycles de transformations au cours desquels il échange du travail et de la chaleur avec l'extérieur.
Si le fluide fournit « effectivement » du travail à l'extérieur, la machine est un moteur.
Si le fluide reçoit du travail et prend de la chaleur à la source froide, la machine thermique est un réfrigérateur (ou un climatiseur).
Si le fluide reçoit du travail et fournit de la chaleur à la source chaude, la machine thermique est une pompe à chaleur.
Si le fluide échange de la chaleur avec deux sources de chaleur, la machine est ditherme.
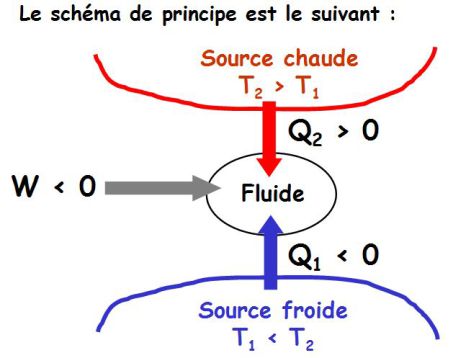
Le cycle du moteur réversible de Carnot (cycle moteur ditherme) :
Le schéma de principe est donné sur la figure suivante.
Le fluide reçoit de la chaleur de la source chaude, fournit du travail au milieu extérieur et rejette une partie de l'énergie calorifique reçue à la source froide (impossibilité du moteur monotherme).
Le cycle est constitué de deux adiabatiques réversibles (pas d'échanges de chaleurs) et de deux isothermes (au contact des deux sources de chaleur). Il est tracé dans le plan de Clapeyron sur la figure suivante.
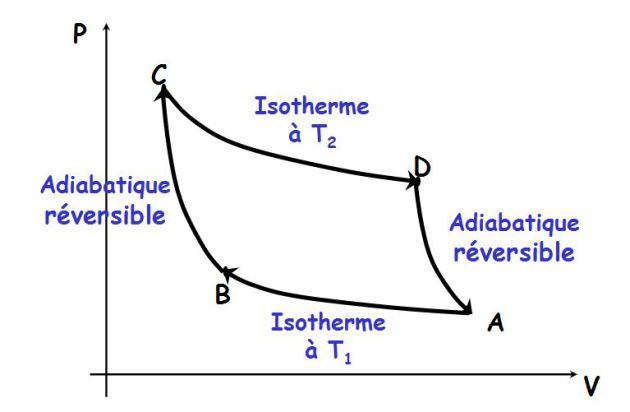
Calcul du rendement :
Le rendement est défini par :
\(\rho = \frac{{travail\;re\c{c}u\;par\;l'exterieur}}{{energie\;calorifique\;fournie}} = - \frac{W}{{{Q_2}}}\)
Où W représente le travail total reçu par le fluide lors du cycle.
D'après le 1er principe :
\(W + {Q_1} + {Q_2} = 0\;\;\;\;\;soit\;\;\;\;\;W = - {Q_1} - {Q_2}\)
D'où :
\(\rho = \frac{{{Q_1} + {Q_2}}}{{{Q_2}}} = 1 + \frac{{{Q_1}}}{{{Q_2}}}\)
Un bilan entropique pour le fluide lors d'un cycle s'écrit :
\(\Delta {S_{cycle}} = \;{S_{echange}} + {S_{creation}}\)
Ävec :
\(\left\{ \begin{array}{l}\Delta {S_{cycle}} = \;0\;\;\;\;\;\;\;\;\;\;\;\;\;\;(le\;long\;d'un\;cycle) \\{S_{echange}} = \frac{{{Q_1}}}{{{T_1}}} + \frac{{{Q_2}}}{{{T_2}}} \\{S_{creation}} = 0\;\;\;\;(transformation\;reversible) \\\end{array} \right.\)
D'où :
\(\frac{{{Q_1}}}{{{T_1}}} + \frac{{{Q_2}}}{{{T_2}}} = 0\;\;\;\;\;(egalite\;de\;Clausius)\)
On en déduit que :
\(\frac{{{Q_1}}}{{{Q_2}}} = - \frac{{{T_1}}}{{{T_2}}}\)
Et :
\(\rho = 1 + \frac{{{Q_1}}}{{{Q_2}}} = 1 - \frac{{{T_1}}}{{{T_2}}}\)
Ce rendement est toujours inférieur à 1 ; par exemple, avec :
\({T_1} = 0^\circ C\;\;;\;\;{T_2} = 100^\circ C\;\;;\;\;\rho = 0,268 = 26,8\% \;!\)
On remarque que ce rendement ne dépend pas de la nature du fluide qui subit le cycle (GP, gaz réel, eau, ...), mais uniquement des températures des sources chaude et froide.
Moteur de Carnot irréversible :
Le cycle de Carnot est désormais irréversible (par exemple, les transferts de chaleur ne se font plus de manière réversible au contact des deux sources de chaleur).
On va montrer que le rendement de ce cycle irréversible est inférieur à celui du cycle réversible, fonctionnant entre les deux mêmes sources.
Un bilan entropique pour le fluide lors d'un cycle s'écrit :
\(\Delta {S_{cycle}} = \;{S_{echange}} + {S_{creation}}\)
Ävec :
\(\left\{ \begin{array}{l}\Delta {S_{cycle}} = \;0\;\;\;\;(le\;long\;d'un\;cycle) \\{S_{echange}} = \frac{{{Q_1}}}{{{T_1}}} + \frac{{{Q_2}}}{{{T_2}}} \\{S_{creation}} > 0\;\;\;\;(transformation\;irreversible) \\\end{array} \right.\)
D'où :
\({S_{echange}} = \frac{{{Q_1}}}{{{T_1}}} + \frac{{{Q_2}}}{{{T_2}}} = - {S_{creation}} < 0\)
Soit l'inégalité de Clausius :
\(\frac{{{Q_1}}}{{{T_1}}} + \frac{{{Q_2}}}{{{T_2}}} < 0\)
Le rendement est toujours défini par :
\(\rho = - \frac{W}{{{Q_2}}} = 1 + \frac{{{Q_1}}}{{{Q_2}}}\)
Mais l'inégalité de Clausius donne :
\(\frac{{{Q_1}}}{{{T_1}}} < - \frac{{{Q_2}}}{{{T_2}}}\;\;\;\;\;soit\;\;\;\;\;\;\frac{{{Q_1}}}{{{Q_2}}} < - \frac{{{T_1}}}{{{T_1}}}\;\;\;\;\;(avec\;{Q_2} > 0)\)
D'où : (théorème de Carnot)
\(\rho = 1 + \frac{{{Q_1}}}{{{Q_2}}} < {\rho _{rev}} = 1 - \frac{{{T_1}}}{{{T_2}}}\)
Machines frigorifiques de Carnot :
Le cycle de Carnot est désormais parcouru dans l'autre sens (sens contraire des aiguilles d'une montre) :
Si on s'intéresse à la source chaude, cette machine frigorifique est une pompe à chaleur.
Si on s'intéresse à la source froide, cette machine frigorifique est un réfrigérateur (ou un climatiseur).
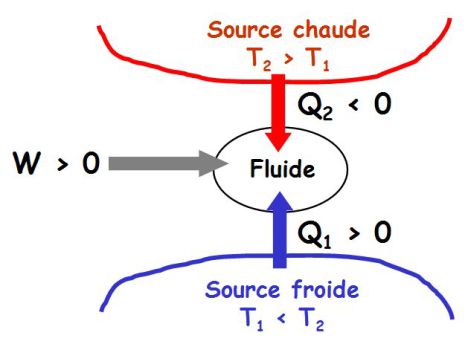
Efficacité d'une machine thermique : (cas réversible)
Réfrigérateur | Pompe à chaleur |
Énergie fournie : W > 0 But : Q1 « grande » Efficacité : \(e = \frac{{energie\;recuperee}}{{energie\;fournie}} = \frac{{{Q_1}}}{W}\) 1er principe : \(W + {Q_1} + {Q_2} = 0\) D'où : \(e = - \frac{{{Q_1}}}{{{Q_1} + {Q_2}}}\) Égalité de Clausius (toujours valable) : \(\frac{{{Q_1}}}{{{T_1}}} + \frac{{{Q_2}}}{{{T_2}}} = 0\;\;\;\;\;;\;\;\;\;\;{Q_2} = - \frac{{{T_2}}}{{{T_1}}}{Q_1}\) D'où : \(e = - \frac{1}{{1 - {T_2}/{T_1}}} = \frac{{{T_1}}}{{{T_2} - {T_1}}}\) | Énergie fournie : W > 0 But : - Q2 « grande » Efficacité : \(e = \frac{{energie\;recuperee}}{{energie\;fournie}} = - \frac{{{Q_2}}}{W}\) 1er principe : \(W + {Q_1} + {Q_2} = 0\) D'où : \(e = \frac{{{Q_2}}}{{{Q_1} + {Q_2}}}\) Égalité de Clausius (toujours valable) : \(\frac{{{Q_1}}}{{{T_1}}} + \frac{{{Q_2}}}{{{T_2}}} = 0\;\;\;\;\;;\;\;\;\;\;{Q_2} = - \frac{{{T_2}}}{{{T_1}}}{Q_1}\) D'où : \(e = \frac{{ - {T_2}/{T_1}}}{{1 - {T_2}/{T_1}}} = \frac{{{T_2}}}{{{T_2} - {T_1}}}\) |
Applications numériques :
Pour un réfrigérateur :
\({T_1} = 300\;K\;\;;\;\;{T_2} = 260\;K\;\;\;\;:\;\;\;\;e = 6,5\)
Pour une pompe à chaleur :
\({T_1} = 293\;K\;\;;\;\;{T_2} = 280\;K\;\;\;\;:\;\;\;\;e = 22,5\)
Ce résultat montre qu'un kWh dépensé pour faire fonctionner la pompe à chaleur fournit autant de chaleur que la dissipation par effet Joule de 22,5 kWh de travail électrique dans un radiateur électrique !
Dans le cas d'un fonctionnement irréversible :
\({e_{refrigerateur}} < \frac{{{T_1}}}{{{T_2} - {T_1}}}\;\;\;\;\;;\;\;\;\;\;{e_{pompe\;a\;chaleur}} < \frac{{{T_2}}}{{{T_2} - {T_1}}}\)