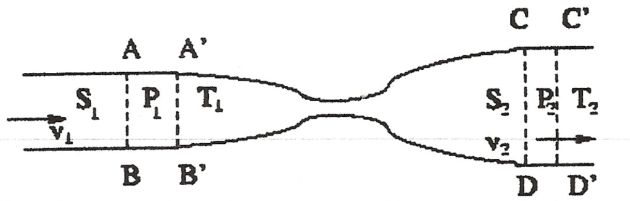
Fluide en écoulement
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Cet exercice n'est pas corrigé.N'hésitez à proposer votre solution sur le forum.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
On considère une vanne calorifugée à travers laquelle circule un fluide (gaz ou liquide).
En amont de la vanne, la section est \(S_1\), la vitesse du fluide est \(v_1\), sa pression \(P_1\), sa température \(T_1\).
En aval, la section est \(S_2\), la vitesse du fluide est \(v_2\), sa pression \(P_2\), sa température \(T_2\).
Ces grandeurs sont supposées uniformes sur toute section droite de la vanne.
Pendant la durée dt, une tranche de fluide passe de la position ABDC à A'B'D'C'.
On suppose l'écoulement stationnaire.
Question
On néglige les énergies cinétique et potentielle du fluide.
Faire un bilan d'énergie interne du fluide, lors du passage de ABDC à A'B'D'C' et calculer \(U_{CDD'C'}-U_{ABB'A'}\) en fonction des variables d'état et de \(V_1=V_{ABB'A'}\) et de \(V_2=V_{CDD'C'}\).
Quelle fonction d'état est conservée lors de cette détente ?
Indice
Utiliser la fiche de cours sur les gaz en écoulement.
Question
Le fluide est un gaz parfait.
Que vaut \(T_2-T_1\) ?
Pourquoi, bien que la transformation soit adiabatique, la loi de Laplace n'est-elle pas vérifiée ?
Calculer la variation d'entropie d'une mole de gaz traversant cette vanne.
Question
Le fluide est du forane, liquide utilisé dans les réfrigérateurs.
En amont, il est liquide, à la température \(\theta_1=20°C\) et à la pression \(P_1=10\;bar\).
En aval, il est partiellement vaporisé et sa température est \(\theta_2=-15°C\) et à la pression \(P_2=3,5\;bar\).
L'enthalpie massique de vaporisation du forane à \(\theta_2\) est \(h_v=65\;kJ.kg^{-1}\).
La capacité thermique massique isobare du forane liquide est : \(c_p=1,3\;kJ.K^{-1}kg^{-1}\).
Calculer la fraction molaire de forane vaporisé.
Question
On ne néglige plus l'énergie cinétique ni l'énergie potentielle du fluide.
Comment sont modifiés les résultats de la 1ère question ? On appellera \(\mu_1\) et \(\mu_2\) les deux masses volumiques et \(u_1\) et \(u_2\) les énergies internes massiques.
Interpréter le résultat obtenu quand on néglige la variation d'énergie interne massique.