Ondes dans une corde
Vibrations transversales d'une corde ; équation d'onde de d'Alembert
On considère une corde inextensible, de masse linéique \(\mu\), tendue horizontalement avec une force constante \(F\).
A l'équilibre, la corde est horizontale.
On supposera dans la suite que la pesanteur n'intervient pas (sinon, la forme de la corde serait une chaînette).
On se propose d'étudier les petits mouvements au voisinage de cet équilibre, avec le modèle suivant :
L'élément de corde situé au point de coordonnées \((x,0)\) à l'équilibre se trouve au point de coordonnées \((x,y(x,t))\) hors équilibre ; autrement dit, on néglige son déplacement le long de (Ox).
L'angle \(\alpha (x,t)\) que fait la tangente à la corde au point d'abscisse \(x\) à l'instant \(t\) est un infiniment petit (\(cos \alpha \approx 1\), \(sin \alpha \approx \alpha\) et \(tan \alpha \approx \alpha\).
Si on considère une coupure fictive au point d'abscisse \(x\), l'action exercée par la partie gauche de la corde sur la partie droite se réduit à une force tangente à la corde notée \(\vec T_g(x,t)\).
De même, l'action exercée par la partie droite sur la partie gauche se réduit à une force \(\vec T_d(x,t)\).
D'après le principe des actions réciproques, \(\vec T_d(x,t)=-\vec T_g(x,t)\).

Le théorème du CI appliqué à un élément de corde situé entre les abscisses \(x\) et \(x+dx\) donne :
\(\mu \;dx\;\frac{{\partial ^2 y}}{{\partial t^2 }}\;\vec u_y = \vec T_g (x,t) + \vec T_d (x + dx,t) = - \vec T_d (x,t) + \vec T_d (x + dx,t)\)
En projection, et en notant \(T = \left\| {\vec T_d } \right\|\) :
\(\left\{ \begin{array}{l}0 = - T(x,t)\cos \alpha (x,t) + T(x + dx,t)\cos \alpha (x + dx,t)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1) \\\mu \;dx\;\frac{{\partial ^2 y}}{{\partial t^2 }} = - T(x,t)\sin \alpha (x,t) + T(x + dx,t)\sin \alpha (x + dx,t)\;\;\;\;\;\;\;\;\;(2) \\\end{array} \right.\)
Si on se limite à l'ordre 1, l'équation (1) donne :
\(T(x + dx) = T(x) = cste = F\)
L'équation (2) se réécrit :
\(\mu \;dx\;\frac{{\partial ^2 y}}{{\partial t^2 }} = - F\alpha (x,t) + F\alpha (x + dx,t) = F\;\frac{{\partial \alpha }}{{\partial x}}\;dx\)
Or :
\(\tan \alpha = \frac{{\partial y}}{{\partial x}} \approx \alpha\)
D'où :
\(\mu \;\frac{{\partial ^2 y}}{{\partial t^2 }} = F\;\frac{{\partial ^2 y}}{{\partial x^2 }}\;\;\;\;\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;\;\;\;\frac{{\partial ^2 y}}{{\partial x^2 }} - \frac{1}{{c^2 }}\frac{{\partial ^2 y}}{{\partial t^2 }} = 0\;\;\;\;\;\;\;\;\;\;(avec\;c = \sqrt {\frac{F}{\mu }} )\)
On retrouve là encore l'équation d'ondes de d'Alembert.
Dans le cas de la corde, l'onde est dite transversale (le déplacement a lieu selon Oy).
Attention : Équation d'onde de d'Alembert
\(\mu \;\frac{{\partial ^2 y}}{{\partial t^2 }} = F\;\frac{{\partial ^2 y}}{{\partial x^2 }}\;\;\;\;\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;\;\;\;\frac{{\partial ^2 y}}{{\partial x^2 }} - \frac{1}{{c^2 }}\frac{{\partial ^2 y}}{{\partial t^2 }} = 0\;\;\;\;\;\;\;\;\;\;(avec\;c = \sqrt {\frac{F}{\mu }} )\)
On retrouve une équation d'ondes de d'Alembert.
La vitesse de propagation de l'onde est :
\(c = \sqrt { \frac {F}{\mu}}\)
La vitesse est d'autant plus grande que la corde est tendue et que la corde est légère.
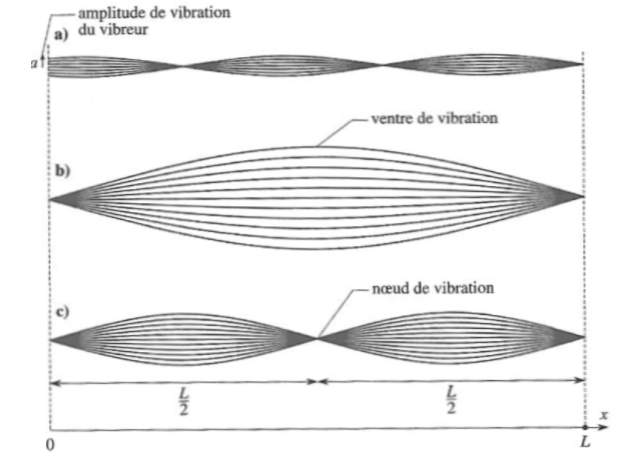
Exemple : Modes propres d'une corde vibrante fixée à ses deux bouts
Exemple : La corde de Melde
Dans l'expérience de Melde, l'extrémité d'abscisse \(x=L\) d'une corde est fixée (\(y(L,t)=0\)) et un opérateur impose en \(x=0\) un déplacement harmonique :
\(y(0,t)=a cos \omega t\)
De pulsation \(\omega\).
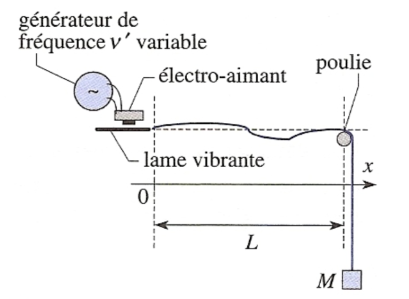
On s'intéresse au régime forcé, obtenu après disparition du régime transitoire.
On cherche ainsi une solution de l'équation de d'Alembert correspondant à une onde stationnaire de même pulsation que l'excitation :
\(y(x,t) = C\;\cos \left( {kx - \psi } \right)\;\cos \left( {\omega t - \varphi } \right)\)
Les conditions aux limites imposent :
\(y(0,t) = Ccos \left( \psi \right)\;\cos \left( {\omega t - \varphi } \right) = a\cos \omega t\)
Et :
\(y(L,t) = 0 = Ccos \left( {kL - \psi } \right)\;\cos \left( {\omega t - \varphi } \right)\)
D'où :
\(a = C\;\cos \left( \psi \right)\;\;\;\;\;\;\;\;\;\;;\;\;\;\;\;\;\;\;\;\;\varphi = 0\;\;\;\;\;\;\;\;\;\;;\;\;\;\;\;\;\;\;\;\;kL - \psi = \frac{\pi }{2}\)
Soit :
\(C = \frac{a}{{\sin (kL)}}\;\;\;\;\;\;\;\;\;\;\;;\;\;\;\;\;\;\;\;\;\;\varphi = 0\;\;\;\;\;\;\;\;\;\;;\;\;\;\;\;\;\;\;\;\;\psi = kL - \frac{\pi }{2}\)
Par conséquent :
\(y(x,t) = a\;\frac{{\sin \left( {k(L - x)} \right)}}{{\sin (kL)}}\;\cos \omega t\;\;\;\;\;\;\;\;\;\;\;\;\;(avec\;k = \frac{\omega }{c})\)
L'amplitude est maximale pour :
\(sin(k(L-x))=\pm 1\)
Et vaut, en valeur absolue :
\(y_{max}=\frac {a}{sin(kL)}\)
Cette amplitude maximale devient infinie (la corde est alors en résonance) pour des pulsations excitatrices telles que :
\(kL = n\pi \;\;\;\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;\;\;\;\omega _n = n\frac{{\pi \;c}}{L}\)
correspondant aux modes propres de la corde.
Néanmoins, d'inévitables amortissements et la raideur de la corde font que l'amplitude maximale garde une valeur finie.
Ainsi l'onde stationnaire devient résonante (en régime forcé) lorsque la pulsation d'excitation du vibreur coïncide avec une des pulsations propres (en régime libre) de vibration de la corde, exactement comme pour un circuit LC série où la pulsation \(\omega_0=1/\sqrt{LC}\) désigne à la fois la pulsation propre en régime libre et la pulsation de résonance en régime forcé.