Équation de conservation de l'énergie
Rappel : Bilan local d'énergie à une dimension (sans ou avec sources)
En l'absence de sources :
On considère un corps homogène (en fait, le plus souvent liquide ou solide) de masse volumique ρ, de conductivité thermique λ et de capacité thermique c. Ces grandeurs sont supposées constantes.
Dans un 1er temps, on suppose qu'il n'y a pas au sein du milieu de sources susceptibles de fournir de la chaleur localement. On reste enfin à une dimension selon (Ox).
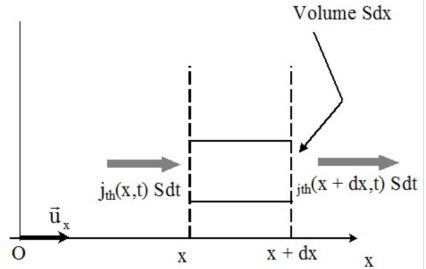
On applique le 1er principe de la thermodynamique à un petit volume dSdx :
\(dU = \delta Q\)
Or :
\(U = \rho dS dx\ c\ T(x,t)\)
Donc :
\(dU = \rho dSdx\ c\ \frac{{\partial T(x,t)}}{{\partial t}}dt\)
Par ailleurs, le flux thermique par conduction est :
\(\delta Q = {j_{th}}(x,t)dSdt - {j_{th}}(x + dx,t)dSdt\)
Ou encore :
\(\delta Q = - \frac{{\partial {j_{th}}(x,t)}}{{\partial x}}dSdtdx\)
Finalement, le 1er principe de la thermodynamique donne :
\(\rho dSdx\ c\ \frac{{\partial T(x,t)}}{{\partial t}}dt = - \frac{{\partial {j_{th}}(x,t)}}{{\partial x}}dSdtdx\)
Finalement : (équation de conservation de l'énergie sans sources)
\(\rho \ c\ \frac{{\partial T(x,t)}}{{\partial t}} = - \frac{{\partial {j_{th}}(x,t)}}{{\partial x}}\)
En présence de sources :
On suppose maintenant la présence de sources de chaleur au sein du milieu ; on note ps(x,t) la puissance volumique dégagée (de manière algébrique) par ces sources.
Exemple (effet Joule) : si le matériau est parcouru par un courant électrique, le volume dSdx, de résistance électrique dR, traversé par le courant électrique di = jdS, reçoit, par effet Joule, pendant la durée dt, l'énergie :
\(\delta Q = dR\;{(di)^2}dt = \frac{1}{\sigma }\frac{{dx}}{{dS}}{j^2}{(dS)^2}dt = \frac{1}{\sigma }{j^2}dxdSdt\)
D'où la puissance volumique due à l'effet Joule :
\({p_s} = \frac{{{j^2}}}{\sigma }\)
En présence de sources, le bilan énergétique devient :
\(\rho dSdx\ c\ \frac{{\partial T(x,t)}}{{\partial t}}dt = - \frac{{\partial {j_{th}}(x,t)}}{{\partial x}}dSdtdx + {p_s}(x,t)dSdxdt\)
Soit :
\(\rho \ c\ \frac{{\partial T(x,t)}}{{\partial t}} = - \frac{{\partial {j_{th}}(x,t)}}{{\partial x}} + {p_s}(x,t)\)
Attention : Bilan local d'énergie à une dimension (sans ou avec sources)
En l'absence de sources :
\(\rho \ c\ \frac{{\partial T(x,t)}}{{\partial t}} = - \frac{{\partial {j_{th}}(x,t)}}{{\partial x}}\)
En présence de sources :
\(\rho \ c\ \frac{{\partial T(x,t)}}{{\partial t}} = - \frac{{\partial {j_{th}}(x,t)}}{{\partial x}} + {p_s}(x,t)\)