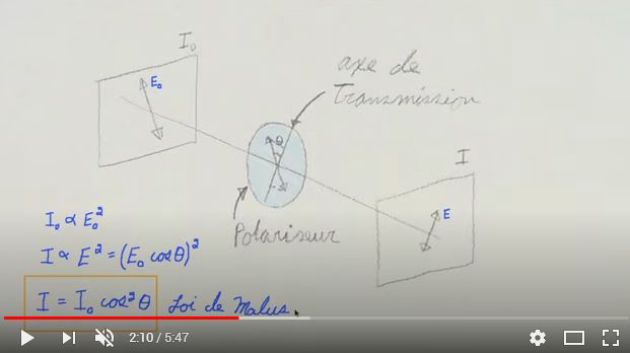
Polarisation des OPPH électromagnétiques
Complément : A video on the polarization of light : Malus' law and Brewster's law
Fondamental : Représentation vectorielle réelle d'une onde plane progressive monochromatique
On considère une onde EM plane progressive monochromatique de pulsation \(\omega\) se propageant dans le vide.
On choisit l'axe (Oz) comme l'axe de propagation, soit \(\vec k=\omega/c \vec u_z\) le vecteur d'onde de l'OPPH.
En notation complexe, le champ électrique de l'onde est :
\(\underline {\vec E} = {\underline {\vec E} _0}\;{e^{i(\omega t - kz)}}\)
On note :
\({\underline {\vec E} _0} = {E_{0x}}{e^{ - i{\varphi _x}}}{\vec u_x} + {E_{0y}}{e^{ - i{\varphi _y}}}{\vec u_y}\)
où \(E_{0x}\) et \(E_{0y}\) sont (moyennant un bon choix des phases \(\varphi_x\) et \(\varphi_y\)) des constantes positives.
De plus, par un choix judicieux de l'origine des temps, on choisira \(\varphi_x=0\) et on notera \(\varphi=\varphi_y\) le déphasage de \(E_y\) par rapport à \(E_y\).
Alors, en notation réelle :
\(\begin{array}{l}{E_x} = {E_{0x}}\cos (\omega t - kz) \\{E_y} = {E_{0y}}\cos (\omega t - kz - \varphi ) \\\end{array}\)
Le champ magnétique s'en déduit (à partir de \(\vec B = \frac{{{{\vec u}_z} \wedge \vec E}}{c})\)) :
\(\begin{array}{l}{B_x} = - \frac{{{E_{0y}}}}{c}\cos (\omega t - kz) \\{B_y} = \frac{{{E_{0x}}}}{c}\cos (\omega t - kz - \varphi ) \\\end{array}\)
Fondamental : Polarisation d'une onde plane progressive monochromatique
La polarisation d'une onde EM est donnée par le comportement de son champ électrique. Plus précisément, la polarisation de l'onde est caractérisée par la trajectoire de l'extrémité du champ électrique de l'onde, dans un plan d'onde.
Pour définir la polarisation d'une onde plane EM progressive harmonique, on se place toujours dans un plan de cote \(z_0\) donnée, que l'on prendra nulle par exemple.
Par conséquent, les coordonnées du champ électrique deviennent :
\(\begin{array}{l}{E_x} = {E_{0x}}\cos (\omega t) \\{E_y} = {E_{0y}}\cos (\omega t - \varphi ) \\\end{array}\)
Polarisation rectiligne :
La polarisation rectiligne correspond au cas où le champ électrique garde une direction constante au cours du temps, que l'on peut choisir parallèle à l'axe (Ox) :
\(\vec E = {E_0}\cos \omega t\;{\vec u_x}\)
Pour un observateur placé dans le plan de cote fixée, le champ oscille en fonction du temps le long de l'axe (Ox).
Polarisation circulaire :
Si \(\varphi=\pm \pi/2\) , les coordonnées \(E_x\) et \(E_y\) du champ électrique sont en quadrature : les axes de l'ellipse qui représente la trajectoire de l'extrémité du vecteur \(\vec E\) coïncident avec les axes (Ox) et (Oy).
Si \(\varphi=+\pi/2\) :
\({E_x} = {E_{0x}}\cos (\omega t)\;\;\;\;\;\;\;et\;\;\;\;\;\;\;{E_y} = {E_{0y}}\sin (\omega t)\)
D'où :
\({\left( {\frac{{{E_x}}}{{{E_{0x}}}}} \right)^2} + {\left( {\frac{{{E_y}}}{{{E_{0y}}}}} \right)^2} = 1\)
C'est bien l'équation d'une ellipse d'axes (Ox) et (Oy), de longueurs \(E_{0x}\) et \(E_{0y}\).
Si de plus les amplitudes \(E_{0x}\) et \(E_{0y}\) sont identiques égales à \(E_0\), l'ellipse correspond à un cercle :
\(E_x^2 + E_y^2 = E_0^2\)
La polarisation de l'onde EM est dite circulaire.
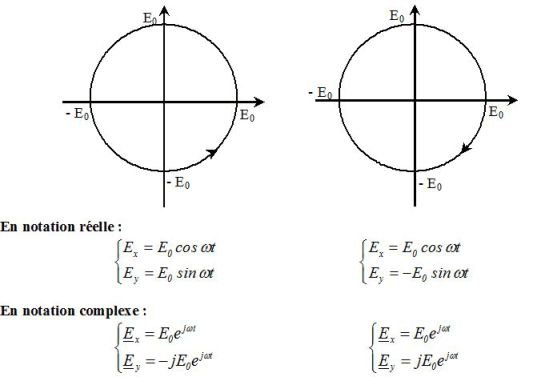
On montre facilement que si \(\varphi=+\pi/2\), l'onde est circulaire gauche et que si \(\varphi=-\pi/2\), l'onde est circulaire droite.
La figure suivante présente à gauche la polarisation circulaire gauche correspondant à \(\varphi=+\pi/2\) et à droite la polarisation circulaire droite correspondant à \(\varphi=-\pi/2\).
Polarisation elliptique :
On rappelle que :
\(\begin{array}{l}{E_x} = {E_{0x}}\cos (\omega t) \\{E_y} = {E_{0y}}\cos (\omega t - \varphi ) \\\end{array}\)
La coordonnée selon (Oy) peut encore s'écrire :
\({E_y} = {E_{0y}}(\cos \omega t\cos \varphi + \sin \omega t\sin \varphi )\)
Afin d'éliminer le temps, on écrit que :
\(\cos (\omega t) = \frac{{{E_x}}}{{{E_{0x}}}}\)
\(\sin \omega t = \frac{1}{{\sin \varphi }}\left( {\frac{{{E_y}}}{{{E_{0y}}}} - \frac{{{E_x}}}{{{E_{0x}}}}\cos \varphi } \right)\)
Par conséquent, en utilisant \({\cos ^2}\omega t + {\sin ^2}\omega t = 1\) :
\({\left( {\frac{{{E_x}}}{{{E_{0x}}}}} \right)^2} + \frac{1}{{{{\sin }^2}\varphi }}\left( {{{\left( {\frac{{{E_y}}}{{{E_{0y}}}}} \right)}^2} - 2\left( {\frac{{{E_y}}}{{{E_{0y}}}}} \right)\left( {\frac{{{E_x}}}{{{E_{0x}}}}} \right)\cos \varphi + {{\left( {\frac{{{E_x}}}{{{E_{0x}}}}} \right)}^2}{{\cos }^2}\varphi } \right) = 1\)
Soit :
\({\left( {\frac{{{E_x}}}{{{E_{0x}}}}} \right)^2} - 2\left( {\frac{{{E_x}}}{{{E_{0x}}}}} \right)\left( {\frac{{{E_y}}}{{{E_{0y}}}}} \right)\cos \varphi + {\left( {\frac{{{E_y}}}{{{E_{0y}}}}} \right)^2} = {\sin ^2}\varphi\)
C'est bien l'équation d'une ellipse en coordonnées cartésiennes.
Cas de la lumière naturelle :
Pour la plupart des sources lumineuses classiques, la lumière émise correspond à une superposition d'OPPM de durées très courtes (de l'ordre de \(10^{-10}s\), mais n'oublions pas que la période des ces ondes est de l'ordre de \(10^{-15}s\)) et de polarisation bien fixée pour chaque onde mais changeant de façon aléatoire entre deux ondes planes progressives monochromatiques.
Les détecteurs optiques sont sensibles à la valeur moyenne dans le temps du carré du champ électrique (c'est l'intensité lumineuse) sur des durées de l'ordre de \(10^{-12}s\) (œil) à \(10^{-6}s\) (bonne cellule photoélectrique).
Ils ne peuvent donc pas suivre la polarisation d'une des OPPM dont la succession forme la lumière visible : on dit que la lumière naturelle n'est pas polarisée.