Premier principe industriel de la thermodynamique
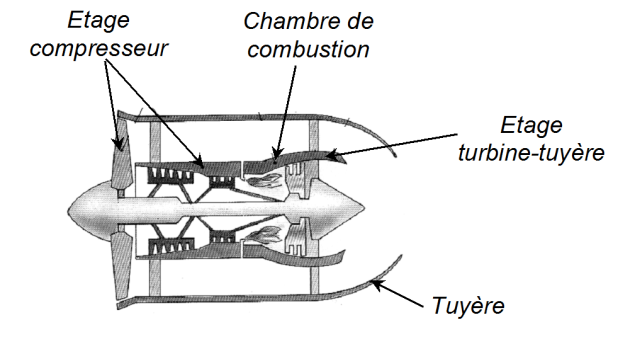
Exemple : Bilans d'énergie interne et d'enthalpie (exemple du moteur à réaction)
Dans un moteur à réaction, un gaz (assimilé à l'air supposé parfait) parcourt un cycle que l'on considérera tout d'abord comme étant réversible.
Il pénètre dans le réacteur à la pression \(P_1\) et à la température \(T_1\) (état (1)).
Il est ensuite comprimé adiabatiquement jusqu'à la pression \(P_2\) et la température vaut alors \(T_2\) (état (2)).
Il rentre alors dans une chambre de combustion où sa température passe de \(T_2\) à \(T_3\), la pression restant égale à \(P_2\) (la sortie de la chambre de combustion est représentée par l'état (3)).
Le gaz subit ensuite une détente adiabatique dans une turbine jusqu'à \(P_4\) et \(T_4\) (état (4)).
Cette détente est telle que la puissance fournie à la turbine compense exactement celle que consomme le compresseur entre les états (1) et (2).
Enfin, le gaz se détend dans une tuyère adiabatique sans parties mobiles jusqu'à \(P_1\) et \(T_5\) (état (5)).
Le gaz est rejeté avec la vitesse \(c\) (ce qui assure la propulsion) dans l'atmosphère extérieure où il se refroidit à la pression constante \(P_1\) de \(T_5\) à \(T_1\).
On considère que la vitesse du gaz est partout négligeable sauf à la sortie de la tuyère.
Données numériques :
\(T_1=290\;K\), \(P_1=1\;bar\), \(P_2/P_1=5\).
La température du gaz à l'entrée de la turbine est \(T_3=1\;300\;K\).
L'air est considéré comme étant un gaz diatomique de masse molaire \(M=29\;g.mol^{-1}\).
Les applications numériques demandées sont relatives à l'unité de masse (ici, 1 kg) et les grandeurs extensives correspondantes seront notées par des lettres minuscules (\(s_m\) pour l'entropie, \(h_m\) pour l'enthalpie, \(e_{cm}\) pour l'énergie cinétique macroscopique,...).
Étude du compresseur
L'unité de masse d'air qui rentre dans le compresseur ne reçoit, de la part de celui-ci, qu'un travail mécanique noté \(w_m\) (avec \(w_m>0\)).
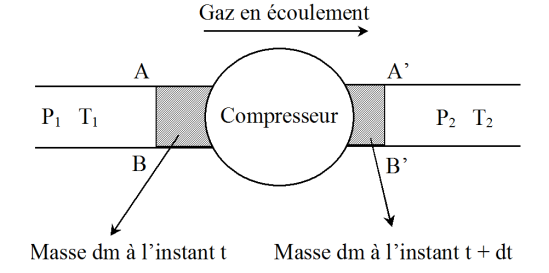
On considère à l'instant \(t\) le système fermé constitué du gaz compris dans le compresseur et de la masse \(dm\) de gaz (dans l'état \(P_1\) et \(T_1\)) qui va rentrer, pendant l'intervalle de temps \(dt\), dans le compresseur.
A l'instant \(t+dt\), ce système est constitué de la même quantité de gaz comprise dans le compresseur et de la même masse \(dm\) de gaz qui est sortie, étant désormais dans les conditions \(P_2\) et \(T_2\).
Le 1er principe appliqué à ce système (en négligeant l'énergie cinétique macroscopique) s'écrit :
\(\left( {U_{gaz\,dans\,le\,compresseur} + (dm)\,u_{m,2} } \right) - \left( {U_{gaz\,dans\,le\,compresseur} + (dm)\,u_{m,1} } \right) = P_1 (dm\,v_{m,1} ) - P_2 (dm\,v_{m,2} ) + (dm)\,w_m\)
Avec :
\(U_{gaz\,dans\,le\,compresseur}\), l'énergie interne du gaz constamment contenu dans le compresseur ; elle est constante en régime stationnaire.
\(u_{m_1}\) et \(u_{m_2}\) désignent les énergies internes massiques et \(v_{m_1}\) et \(v_{m_2}\) les volumes massiques de l'air dans les états (1) et (2) respectivement.
La quantité \(P_1(dmv_{m_1})-P_2(dmv_{m_2})\) représente le travail des forces de pressions extérieures au système, à l'entrée et à la sortie de la machine (encore appelé travail de transvasement).
Enfin, le transfert thermique reçu par le système est nul puisque, d'une part, le compresseur est calorifugé et, d'autre part, il n'y a pas de transfert de chaleur par conduction entre la masse qui rentre ou qui sort de la machine et son environnement immédiat puisque les températures sont identiques (et égales à \(T_1\) ou \(T_2\)).
En remarquant que :
\(h_m=u_m+Pv_m\)
représente l'enthalpie massique, on aboutit finalement au bilan énergétique suivant :
\(h_{m,2} - h_{m,1} = w_m\)
Étude de la tuyère
Le bilan énergétique dans la tuyère s'écrit maintenant, puisque l'énergie cinétique macroscopique en sortie \(e_{cm,5}\) n'est plus négligeable (et avec des notations semblables à celles du paragraphe précédent) :
\(\left( {U_{gaz\,dans\,la\,tuyere} + (dm)\,u_{m,5} + (dm)\,e_{cm,5} } \right)-\left( {U_{gaz\,dans\,la\,tuyere}+(dm)\,u_{m,4} } \right) =P_4 (dm\,v_{m,4} ) - P_1 (dm\,v_{m,5} )\)
Soit :
\(\left( {h_{m,5} - h_{m,4} } \right) + e_{cm,5} = 0\;\;\;\;\;soit\;\;\;\;\;e_{cm,5} = - \left( {h_{m,5} - h_{m,4} } \right) = - \frac{7}{2}r\,\left( {T_5 - T_4 } \right)\)
Attention : Premier principe industriel
\(h_m\), \(e_{c,macro}\) et \(e_{p,ext}\) désignent l'enthalpie massique, l'énergie cinétique macroscopique et l'énergie potentielle massique de pesanteur du fluide en écoulement.
\(w_m\) représentent le travail massique reçu par le fluide dans la machine (en dehors des forces de pression à l'entrée et à la sortie de la machine). Il est encore appelé "travail utile massique".
\(q_m\) est le transfert thermique massique reçu par le fluide lors de son passage dans la machine.
Le premier principe industriel s'écrit, pour un fluide en écoulement :
\(\Delta h_m + \Delta e_{c,macro} + \Delta e_{p,ext} = w_m + q_{th}\)