La complexité de l'équation de Navier - Stokes :

\(\rho \left[ {\frac{{\partial \vec v}}{{\partial t}} + \left( {\vec v.\overrightarrow {grad} } \right)\vec v} \right] = - \overrightarrow {grad} P + \rho \vec g + \eta \Delta \vec v\)

est due essentiellement à deux termes :

• Le terme de convection de quantité de mouvement \((\vec v.\overrightarrow {grad} )\vec v\), qui rend l'équation non linéaire.

• Le terme de diffusion visqueuse \(\eta \Delta \vec v\) dû au transfert de quantité de mouvement, qui introduit des dérivées du second ordre.

On considère un écoulement dont les paramètres sont \(v_{\infty}\) (vitesse du fluide loin de l'obstacle) et \(D\) une taille caractéristique (la longueur de l'obstacle, par exemple).

L'ordre de grandeur du rapport du terme convectif sur le terme de diffusion vaut :

\(\frac{{\left\| {\rho (\vec v.\overrightarrow {grad} )\vec v} \right\|}}{{\left\| {\eta \Delta \vec v} \right\|}} \approx \frac{{\rho \frac{{v_\infty ^2 }}{D}}}{{\eta \frac{{v_\infty }}{{D^2 }}}} = \frac{{\rho Dv_\infty }}{\eta }\)

Avec \(\nu = \frac{\eta }{\rho }\) ((viscosité dynamique du fluide) :

\(\frac{{\left\| {\rho (\vec v.\overrightarrow {grad} )\vec v} \right\|}}{{\left\| {\eta \Delta \vec v} \right\|}} \approx \frac{{Dv_\infty }}{\nu } = R_e\)

\(R_e\) est le nombre de Reynolds.

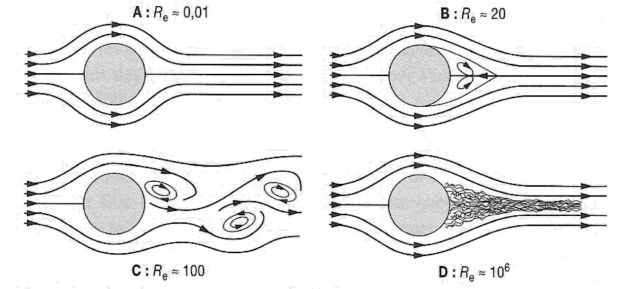
L'expérience montre que si \(R_e<2\;000\), l'écoulement est laminaire alors que si \(R_e>4\;000\), il devient facilement turbulent.

Pour un nombre de Reynolds élevé, les transferts de quantité de mouvement par convection sont plus importants que ceux par diffusion ; cela signifie que le temps caractéristique associé à ces transferts par convection est plus court que celui par diffusion.

Tout se passe comme si la viscosité du fluide était nulle. Le fluide a un comportement de fluide parfait et son mouvement est régi par l'équation d'Euler :

\(\rho \;\frac{{\partial \vec v}}{{\partial t}} + \rho \;(\vec v.\overrightarrow {grad} )\;\vec v = - \overrightarrow {grad} P\; + \vec f_v\)

L'épaisseur de la couche limite \(\delta \approx \frac{L}{{\sqrt {R_e } }}\) est alors faible.

Pour un nombre de Reynolds faible, les transferts de quantité de mouvement par diffusion sont plus importants que ceux par convection ; le temps caractéristique associé à ces transferts par diffusion est plus court que par convection.

L'équation de Navier-Stokes devient alors :

\(\rho \;\frac{{\partial \vec v}}{{\partial t}} = - \overrightarrow {grad} P\; + \vec f_v + \eta \Delta \vec v\)

Les écoulements dominés par la viscosité sont toujours des écoulements très lents avec une longueur caractéristique très courte (sève dans les pores des arbres) ou impliquant des fluides très visqueux (écoulements de lave).

Le terme convectif est non linéaire : l'apparition de turbulences a lieu pour des nombres de Reynolds élevés, donc lorsque le terme non linéaire l'emporte nettement sur le terme linéaire (dû à l'aspect diffusif de l'écoulement, c'est-à-dire à la viscosité).

C'est donc bien l'aspect non linéaire de l'écoulement qui favorise les turbulences.