Loi d'Ohm locale
Méthode : Présentation du modèle de Drude (1900)
Dans un conducteur métallique (« ohmique ») soumis à une tension électrique, les électrons de conduction se mettent en mouvement.
On définit l'intensité I du courant électrique et le vecteur \(\vec j\) densité de courant électrique :
\(I = \frac{{dq}}{{dt}}\;\;\;\;\;;\;\;\;\;\;\vec j = {\rho _m}\vec v\;\;\;\;\;\;\;;\;\;\;\;\;\;\;I =\iint_{(S)}\vec j . \vec n dS\)
Avec :
\(\rho_m\) : densité de charges mobiles (\(\rho_m=nq\), où \(n\) est la densité de charges mobiles).
\(\vec v\) : vitesse des porteurs de charge \(q\)
Soit \(\vec E\) le champ électrique responsable de la mise en mouvement des charges mobiles.
Une charge mobile est d'une part soumise à la force électrique :
\({\vec f_{el}} = q\vec E\)
Elle est également soumise à une force due aux charges fixes qui composent le réseau cristallin du conducteur métallique.
On modélise cette force par une force de type « frottement fluide » :
\({\vec f_{res}} = - k\vec v\)
où k est une constante phénoménologique, dépendant du conducteur ohmique considéré.
Fondamental : Loi d'Ohm locale et conductivité d'un conducteur ohmique
Le PFD appliqué (dans le référentiel du laboratoire) à une charge mobile donne alors (m désigne la masse d'un porteur de charge) :
\(m\frac{{d\vec v}}{{dt}} = q\vec E - k\vec v\;\;\;\;\;soit\;\;\;\;\;\frac{{d\vec v}}{{dt}} + \frac{k}{m}\vec v = \frac{q}{m}\vec E\)
On pose :
\(\frac{1}{\tau } = \frac{k}{m}\)
Avec \(\tau\) le temps de relaxation du milieu ohmique.
L'équation différentielle devient :
\(\frac{{d\vec v}}{{dt}} + \frac{1}{\tau }\vec v = \frac{q}{m}\vec E\)
Si l'on suppose le champ électrique constant (indépendant du temps), la solution de cette équation différentielle est :
\(\vec v = \vec A\exp ( - \frac{t}{\tau }) + \frac{{q\tau }}{m}\vec E\)
En régime permanent (pour \(t>>\tau\)) :
\(\vec v = \frac{{q\tau }}{m}\vec E\)
Le vecteur densité de courant s'en déduit :
\(\vec j = nq\vec v = \frac{{n{q^2}\tau }}{m}\vec E\)
On pose :
\(\sigma = \frac{{n{q^2}\tau }}{m}\)
la conductivité électrique du milieu.
Attention : Loi d'Ohm locale
Pour un conductivité ohmique de conductivité \(\sigma\) (et de résistivité électrique \(\rho=1/\sigma\)) :
\(\vec j = \sigma \vec E = \frac {1}{\rho} \vec E\)
La loi d'Ohm locale est ainsi expliquée à partir de la limitation de la vitesse de migration des porteurs du fait de leurs interactions avec le milieu matériel (les cations fixes du réseau métallique).
Ordres de grandeur :
Les porteurs de charge sont des électrons.
Le tableau suivant donne les conductivités de quelques métaux usuels à température ambiante (300 K) :
Métaux | Ag | Cu | Au | Al | Hg |
\(\sigma\;(10^7S.m^{-1})\) | 6,21 | 5,88 | 4,55 | 3,65 | 0,10 |
Pour le cuivre, on peut évaluer le temps de relaxation :
\(\tau = {2,4.10^{ - 14}}\;s\)
Le régime permanent est atteint très rapidement, du moins tant que les durées caractéristiques de variations du champ \(\vec E\) sont très supérieures à \(10^{-14}s\).
Ainsi, la loi d'Ohm locale restera valable tant que les fréquences du champ électrique ne seront pas trop élevées (c'est l'ARQS, approximation des régimes quasi-stationnaires).
Complément : Résistance électrique et loi d'Ohm macroscopique
On considère un conducteur ohmique cylindrique de section transverse \(S\) et de longueur \(L\) (un fil électrique en cuivre, par exemple).
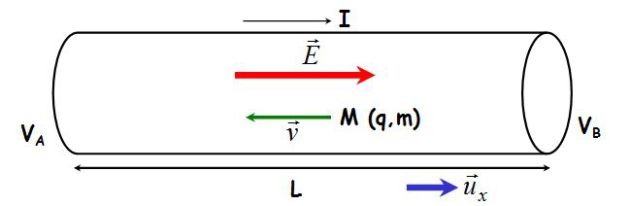
Le champ à l'intérieur du fil est (en régime indépendant du temps) :
\(\vec E = \frac{{{V_A} - {V_B}}}{L}\;{\vec u_x}\)
D'après la loi d'Ohm locale :
\(\vec j = \sigma \vec E\)
Par ailleurs :
\(I=\iint_S\vec j.\vec n dS\)
D'où :
\(I = \sigma ES = \sigma S\frac{{{V_A} - {V_B}}}{L}\;\;\;et\;\;\;{V_A} - {V_B} = \frac{L}{{\sigma S}}I\)
On pose :
\(R = \frac{L}{{\sigma S}}=\frac{\rho L}{S}\)
la résistance électrique du fil.
Alors (en convention récepteur) :
\({V_A} - {V_B} = RI\;\;\;\;\;(Loi\;d'Ohm\;macroscopique)\)