Étude de filtres du 2nd ordre en électricité
Attention :
Quelques vidéos pour illustrer les filtres du 2nd ordre
Méthode : Filtre passe-bande (résonance d'intensité)
Aspect expérimental :
Réaliser le montage expérimental en précisant aux bornes de quel composant il faut se placer pour avoir un filtre passe-bande.
Justifier qualitativement votre choix.
Choisir les valeurs de \(L\) et de \(C\) pour avoir une fréquence de résonance de l'ordre de \(500\;Hz\).
Régler la valeur de la résistance \(R\) afin d'avoir un facteur de qualité "correct".
Tracer le diagramme de Bode en amplitude et en phase, sur papier millimétré.
Comment mettre en évidence expérimentalement la résonance en mode XY ?
En déduire, expérimentalement, la fréquence de résonance \(f_0\), la bande passante \(\Delta f\) et le facteur de qualité \(Q=f_0/\Delta f\).
Quelle est l'influence de \(R\) sur la bande passante ?
Quelle est la résistance interne de la bobine ?
Mise en évidence de la surtension : se placer à la résonance (appelée ici résonance d'intensité) et mesurer, avec un multimètre, les tensions aux bornes de la bobine et du condensateur.
Sont-elles plus grandes que celle délivrée par le GBF ?
Aspect théorique :
Afin d'interpréter les résultats expérimentaux, on pourra utiliser les rappels théoriques suivants :
Le gain et l'argument de la fonction de transfert du filtre \(\underline H (j\omega ) = \frac{{{{\underline v }_s}}}{{{{\underline v }_e}}}\)
sont donnés par :
\(G(\omega ) = \frac{R}{{\sqrt {{{(R + r)}^2} + {{(L\omega - 1/C\omega )}^2}} }}\;\;\;\;\;et\;\;\;\;\;\tan \varphi = - \frac{{L\omega - 1/C\omega }}{{R + r}}\)
où \(r\) est la résistance interne de la bobine.
Le gain à la résonance d'intensité (obtenue pour \(f_0=1/2\pi\sqrt{LC}\)) vaut :
\(G(f_0)=\frac{R}{R+r}\)
A la résonance, la tension maximale aux bornes du condensateur est : (\(E\) est la tension maximale du GBF)
\(U_C=I/(C\omega_0)=\frac{U_R}{RC\omega_0}=\frac{1}{(R+r)C\omega_0}E=QE\)
Où :
\(Q=(R+r)C\omega_0=(R+r)/L\omega_0\)
est le facteur de qualité du circuit.
On montre de même que :
\(U_L=QE\)
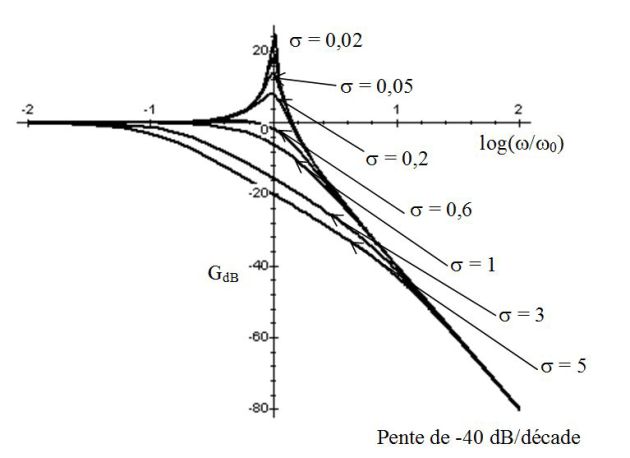
Méthode : Filtre passe-bas (résonance de charge)
Méthode : Filtre passe-haut
Méthode : Filtre réjecteur de bande (ou coupe-bande)
Simulation : Animations JAVA de Jean-Jacques Rousseau (Université du Mans)
Suspension d'un véhicule : cliquer
Circuits RC, filtres, dérivateurs et intégrateurs : cliquer
Filtres passifs : cliquer
Filtres passifs (2) : cliquer
Filtres passifs en L, T et Pi : cliquer
Filtres passifs du second ordre : cliquer
Filtres passifs en T et T ponté : cliquer
Filtre en double T ponté : cliquer
Filtre deux voies : cliquer
Complément : Une vidéo pour aller plus loin ...
Apprendre la Réponse d'un Système